б) Способы задания операций

Часто операция на множестве задается текстовой формулировкой. На конечном множестве операция может задаваться таблицей. В этом случае элементы множества записываются в верхней строке и в том же порядке в левом столбце таблицы, а на пересечении строк и столбцов записывается результат выполнения операции над соответствующими элементами данного множества.

Пример 1.

Составим таблицу композиции на множестве поворотов равностороннего треугольника вокруг его центра, приводящих его к самосовмещению.

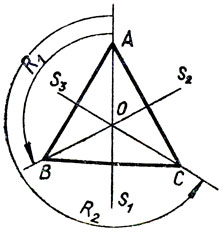
Рис. 5

Вращая треугольник ABC в своей плоскости вокруг центра O (см. рисунок 5), можно получить три его различных положения (рис. 6).

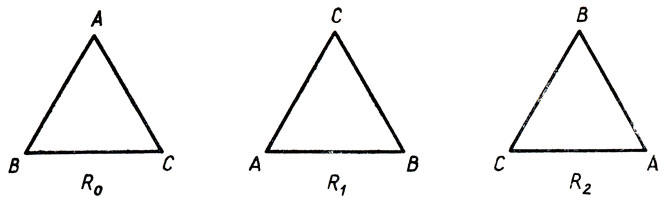
Рис. 6

Обозначим все повороты этого треугольника вокруг центра в его плоскости, приводящие треугольник к самосовмещению:

R₀ - поворот на угол в 0°;

R₁ - поворот на угол в 120°, переводящий А в 5;

R₂ - поворот на угол в 240°, переводящий А в С (рис. 5, 6).

Композицией поворотов R₂ и R₂ является поворот R₁, так как R₂•R₂=R₁. Действительно, последовательное выполнение двух поворотов треугольника ABC вокруг центра O, каждый из которых есть поворот на 240°, совпадает с поворотом его из начального положения вокруг центра O на угол 120°, т. е. совпадает с поворотом R₁. Аналогично можно найти все возможные композиции двух элементов из множества {R₀, R₁, R₂}.

В результате получим таблицу 2 (с. 46). Из нее видно, что композиция поворотов равностороннего треугольника вокруг центра является операцией на множестве этих поворотов.

Пример 2.

Возьмем множество, состоящее из трех элементов, например {1, 2, 3}. Их можно расположить по порядку шестью способами:

123; 132; 213; 231; 312; 321.

Говорят, что возможны шесть перестановок из трех элементов. Запишем одну под другой две любые перестановки из трех элементов (123/132)

Две перестановки, записанные таким образом, дают обратимое отображение множества {1, 2, 3} на себя. Это отображение называют подстановкой третьей степени (по числу элементов множества). Аналогично можно определить и подстановку степени n.

Обозначим подстановки 3-й степени, а их всего 3! = 1•2•3=6, (123/123), (123/231), (123/312), (123/132), (123/321), (123/213) одинаковы и имеют одно и то же обозначение P₃, так как во всех этих перестановках 1 переходит в 1, 2 - в 3, а 3 - в 2.

Умножением подстановок 3-й степени (n-й степени) назовем новую подстановку той же степени, производящую такое изменение в расположении элементов 1; 2; 3 (1; 2; 3; ...; n), которое получается в результате последовательного выполнения этих двух подстановок. Например, (123/312) * (123/132) = (123/213).

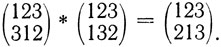
Таблица 2

Действительно, посредством подстановки P₂ 1 переходит в 3, посредством подстановки P₃ 3 переходит в 2; посредством подстановки P₂ 2 переходит в 1; а посредством подстановки P₃ 1 переходит в 1 и т. п. Подстановка P₅ переводит 1 в 2, 2 в 1 и т. д.; она и будет произведением двух первых подстановок. Нетрудно убедиться, что определенное таким образом умножение подстановок 3-й степени является операцией на множестве подстановок 3-й степени с таблицей умножения, представленной таблицей 3.

Таблица 3

Упражнения

3. Найдите произведение подстановок: а) P₀ и P₃; б) P₃ и P₂; г) P₁ и P₄. Результаты сверьте с таблицей 2.

4. По таблице 2 найдите произведение подстановок: а) P₃ и P₁; б) P₁ и P₃; в) P5 и P₅; г) P₁, P₃ и P₅.

5. Объясните, почему умножение подстановок 3-й степени есть операция на множестве этих подстановок.

6. Составьте таблицу умножения подстановок 2-й степени.

7. {R₀, R₁, R₂, S₁, S₂, S₃} - множество самосовмещений равностороннего треугольника ABC, где R₀, R₁, R₂ - повороты вокруг его центра O соответственно на 0°, 120° и 240°, S₁ - симметрия с осью AO, переводящая B в C, а C в B, S₂ и S₃ - две другие осевые симметрии (рис. 5). Составьте таблицу композиции самосовмещений равностороннего треугольника. Является ли операцией композиция самосовмещений равностороннего треугольника?

8. {R₀, R₁, R₂, R₃} - множество поворотов квадрата ABCD вокруг центра O (рис. 7). Составьте таблицу композиции поворотов на данном множестве. Является ли эта композиция операцией?

9. Составьте таблицу композиции самосовмещений квадрата ABCD на множестве {R₀, R₁, R₂, R₃, S₁, S₂, S₃, S₄} (рис. 7).

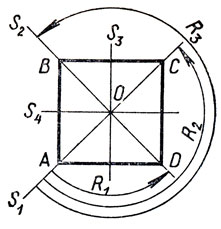
Рис. 7

10. Составьте таблицу композиции на множестве {R₀, R₁, S₁, S₂} - множестве самосовмещений прямоугольника ABCD (рис. 8).

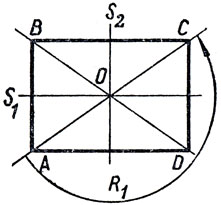
Рис. 8

11. Являются ли примерами операции композиции самосовмещений квадрата и прямоугольника?