Обучение обобщению и конкретизации при изучении понятий в VI-VIII классах

В связи с увеличением запаса геометрических сведений и развитием, совершенствованием навыков проведения дедуктивных рассуждений в процессе изучения систематического курса геометрии учащимися VI-VIII классов и повышением логического уровня изложения материала работа по обучению обобщению и конкретизации при изучении геометрических понятий в этих классах может принимать все более явный и четкий характер. В этих классах могут быть более полно и более явно представлены все перечисленные в пункте 1 типы задач (1-8).

В VI-VIII классах продолжают использоваться термины, выражения, используемые в IV-V классах (см. начало предыдущего пункта). Это объясняется тем, что эти выражения позволяют осознавать сущность той работы, которая проводится при обучении обобщению и конкретизации. Однако вместе с тем в VI-VIII классах вводятся и новые термины, выражения. ("Старая" терминология IV-V классов выполняет теперь еще одну функцию: она способствует овладению и осознанию новой терминологии.) Так, в VI классе можно использовать такие выражения: "Можно ли доказать "это" свойство с помощью указанных свойств?"; "Является ли "это" свойство следствием "таких-то" свойств?"; "На основе "указанных" свойств доказано "данное свойство", что это значит?".

В VII классе можно постепенно перейти к использованию выражений: "Это" свойство не зависит от "этих" свойств (т. е. выполнение "данных" свойств не означает, что "это" свойство выполняется); "это" свойство - следствие этих свойств; докажите независимость "этого" свойства от указанных свойств; докажите непротиворечивость "таких-то" свойств. Наряду с выражениями вида "Множество параллелограммов шире множества прямоугольников", "Множество параллелограммов есть собственное подмножество множества четырехугольников" можно употреблять более краткие выражения: "Параллелограмм - обобщение прямоугольника"; "Прямоугольник - конкретизация понятия параллелограмма"; "Параллелограмм - конкретизация понятия четырехугольника".

Рассмотрим ряд задач на обучение обобщению и конкретизации при изучении понятий в VI-VII классах.

При введении понятия расстояния в VI классе указываются три его свойства (см. учебное пособие по геометрии А. Н. Колмогорова и др.). Множество этих свойств и есть первичное содержание понятия расстояния (они входят в определение расстояния). Следовательно, свойства, принадлежащие первичному содержанию понятия, здесь уже перечислены.

Из свойств, входящих в производное содержание понятия расстояния, в учебном пособии указывается одно:

4) Для любых трех точек A, B, C расстояние |AB| не меньше разности расстояний |AC| и |BC|

Пользуясь перечисленными свойствами расстояния, можно предложить, например, следующие задачи на обучение обобщению и конкретизации.

15. На берегу реки расположены три населенных пункта A, B и C. Условимся под расстоянием от одного пункта до другого подразумевать время движения от первого из них до второго на лодке. Все ли свойства расстояния будут в этом случае выполняться? Обязательно ли выполняется 2-е свойство расстояний, если выполняются свойства 1 и 3? Можно ли указанное время движения на лодке считать расстоянием? Почему? Можно ли было считать это время расстоянием, если бы свойство 2 расстояний не указывалось?

Данная задача позволяет нам установить независимость свойства 2 от свойств 1 и 3. Учащиеся, решив эту задачу, начинают осознавать, что дополнение свойств 1 и 3 приводит к тому, что некоторые величины, которые до этого можно было считать расстоянием (в данном случае - время движения по реке), после включения свойства 2 расстоянием считать нельзя. Таким образом, устанавливается "конкретизирующее воздействие" свойства 2 расстояний по отношению к свойствам 1 и 3. В результате решения этой задачи устанавливается также (неявно) непротиворечивость свойств 1 и 3.

16. Дан ΔABC, причем A=20°, B=40°, C=120°. Можно ли за расстояние между двумя вершинами треугольника принять величину угла при третьей вершине (т. е. считать, что |AB|=120, |AC|=40, |BC|=20)? Почему?

При решении предложенной задачи устанавливается независимость свойства 3 от свойств 1 и 2. Неявно учащиеся осознают, что дополнение свойств 1 и 2 свойством 3 "что-то меняет", уменьшает число случаев, когда та или иная величина может быть принята за расстояние. Эта задача способствует усвоению необходимого и 32 достаточного условия конкретизации и обобщения при включении или исключении свойства.

При изучении осевой симметрии можно предложить следующие задачи на обучение обобщению и конкретизации.

17. Перечислить свойства осевой симметрии, указанные в определении этого понятия.

В результате решения задачи выделяем следующие свойства:

1) Осевая симметрия - это перемещение.

2) Существует прямая l, все точки которой остаются на месте.

3) Полуплоскости с границей l отображаются одна на другую.

Множество этих свойств есть первичное содержание понятия осевой симметрии.

Изучение осевой симметрии в V классе и использование физической модели осевой симметрии в виде перегибания листа бумаги относительно прямой убеждает учащихся в непротиворечивости свойств 1-3. В последующих задачах целесообразно показать независимость перечисленных свойств друг от друга и этим подвести учащихся к осознанию их конкретизирующей роли.

18. Всякое ли перемещение является осевой симметрией? Отрицательный ответ на этот вопрос говорит о независимости свойств 2 и 3 от свойства 1 и "важности" свойств 2 и 3.

19. Каждую точку плоскости отобразим на себя. (Такое отображение называется тождественным.) Какие свойства осевой симметрии для такого отображения выполняются? не выполняются? Почему это отображение нельзя считать осевой симметрией? Можно ли свойство 3 осевой симметрии доказать с помощью первых двух свойств?

Эта задача - на установление независимости свойства 3 осевой симметрии от свойств 1 и 3.

20. А - множество перемещений, обладающих свойством 2, В - множество осевых симметрий. Какое из этих двух множеств есть собственное подмножество другого? Почему? Изобразите эти множества диаграммами Эйлера.

21. Какими из указанных трех свойств осевой симметрии обладает центральная симметрия?

Здесь доказывается независимость свойства 2 осевой симметрии от свойств 1 и 3. Как и в предшествующем случае, используем эту задачу для сравнения объемов двух понятий.

22. A - множество осевых симметрий, B - множество перемещений, обладающих свойством 3. Какие из отношений верны:

а) B⊂A, б) A=B, в) A⊂B, г) A⊂B, A≠B, д) A⊂B, A∩B≠∅, е) A∪B=B? Изобразите эти множества диаграммами Эйлера.

В только что предложенной задаче неявно устанавливается, какое из двух понятий есть конкретизация (обобщение) другого.

В задачах 16-21 использовались свойства, входящие в определение (первичное содержание) осевой симметрии. Для обучения обобщению и конкретизации целесообразно использовать также следствия первичного содержания (свойства, входящие в производное содержание). Поэтому целесообразно предложить следующую задачу.

23. Найдите несколько свойств осевой симметрии, не указанных а определении (вытекающих из свойств, входящих в определение).

Пусть выделены следующие свойства:

4) Существует бесконечное множество прямых, отображающихся на себя.

5) Существует окружность, отображающаяся на себя.

Выделенные свойства в неявном виде дают учащимся представление о производном содержании, о содержании понятия. Ими можно воспользоваться для продолжения обучения обобщению и конкретизации.

24. А - множество осевых симметрий, В - множество перемещений, обладающих свойствами 2-5. Изобразите оба множества с помощью диаграммы Эйлера.

Здесь учащиеся устанавливают, что включение в определение (в первичное содержание) нового свойства не приводит к конкретизации понятия. Этим самым они подводятся к осознанию необходимого и достаточного условия получения конкретизации понятия при включении нового свойства.

25. Какими из свойств 1-5 осевой симметрии обладает центральная симметрия? A - множество осевых симметрий, B - множество перемещений, обладающих свойствами 3-5. Верно ли, что

а) B⊂A, б) A=B, в) A⊂B?

26. A - множество центральных симметрий, B - множество перемещений, обладающих свойствами 4 и 5. Какое из этих множеств есть подмножество другого? Почему?

Данная задача - на установление, какое из двух понятий есть конкретизация (обобщение) другого.

27. Каково множество перемещений, которые являются осевыми симметриями и обладают свойством: "Не существует окружности, которая отображается на себя".

Ответ: ∅. Эта задача - на установление противоречивости свойств.

Выделение других свойств-следствий, содержащихся в определении, приводит к большому числу разнообразных задач на обучение обобщению и конкретизации.

Большие возможности обучения обобщению и конкретизации имеются при изучении понятий параллелограмма, прямоугольника, ромба, квадрата (VII класс). Рассмотрим это для случая параллелограмма.

Сначала предлагаем задачу на перечисление свойств, принадлежащих первичному содержанию понятия параллелограмма.

28. Перечислить свойства параллелограмма, указанные в его определении.

Эти свойства следующие:

1) Параллелограмм - это четырехугольник.

2) Противоположные стороны параллелограмма параллельны.

Введение понятия параллелограмма обычно начинается с демонстрации соответствующих рисунков, моделей, что означает не что иное, как установление непротиворечивости свойств, входящих в определение (первичное содержание). После перечисления свойств, принадлежащих первичному содержанию, целесообразно предложить учащимся построить параллелограмм, т. е. четырехугольник, обладающий свойством 2. Еще раз убедившись построением в существовании такого четырехугольника, учащиеся осознают непротиворечивость свойств 1 и 2. Эту цель и преследует следующая задача.

29. Построить четырехугольник, противоположные стороны которого параллельны.

Далее учащиеся убеждаются в независимости свойств, входящих в определение параллелограмма. Это делается при решении следующей задачи.

30. а) Постройте четырехугольник, не обладающий свойством 2.

б) Постройте многоугольник, обладающий свойством 2, но не обладающий свойством 1.

В процессе решения пункта а) этой задачи учащиеся осознают, что свойство 2 выделяет из множества четырехугольников его собственное подмножество - множество параллелограммов. Это означает, что неявно учащимися осознается непротиворечивость и независимость свойств - достаточное условие конкретизации. Таким образом, при решении двух последних задач учащиеся подготавливаются к пониманию необходимого и достаточного условия конкретизации.

Решение пункта б) предложенной задачи подводит учащихся к пониманию, что замена одного свойства (быть четырехугольником) другим (быть многоугольником) может, как в данном случае, привести к другому понятию. Они осознают, что от замены множества четырехугольников более широким множеством - множеством многоугольников - получили новое понятие, содержащее более широкое множество объектов, чем прежнее. А это есть не что иное, как знакомство с еще одним доступным способом обобщения понятия. Чтобы сделать осознание этих фактов более явным, предлагаем следующую задачу.

31. A - множество четырехугольников, обладающих свойством 2, B - множество многоугольников, обладающих свойством 2. Изобразите эти множества диаграммами Эйлера. Какие высказывания верны: а) B⊂A; б) B=A; в) A⊂B, A≠B?

После решения рассмотренных задач можно ввести явно термины "обобщение", "конкретизация". Для этого предлагаем изобразить диаграммами Эйлера множество M четырехугольников и множество P параллелограммов. Затем надо подвести итог: множество четырехугольников более широкое, чем множество параллелограммов (P⊂M, P≠M). Это высказывают иногда иначе: "Четырехугольник есть обобщение параллелограмма" (т. е. фигура более "общая" - она может быть и параллелограммом, и непараллелограммом). Говорят также и иначе: "Параллелограмм - конкретизация четырехугольника" (частный, конкретный случай четырехугольника). Необходимо записать: "Четырехугольник - обобщение понятия параллелограмма"; "Параллелограмм - конкретизация понятия четырехугольника". После этого надо предложить выяснить, какое из двух понятий, рассмотренных в последней задаче (многоугольника с параллельными противоположными сторонами и параллелограмма), есть обобщение другого; конкретизация другого.

Введение терминов "обобщение", "конкретизация" не должно быть навязчивым. Учащиеся должны привыкать к ним постепенно. Достоинство ответа: "Множество четырехугольников - более широкое, чем множество параллелограммов" или "Множество параллелограммов есть собственное подмножество множества четырехугольников" вместо "Четырехугольник - это обобщение параллелограмма" - нельзя считать уменьшенным. Наиболее целесообразно использовать эту терминологию параллельно. Этим самым правильно постепенно осознаются термины "обобщение" и "конкретизация". В то же время введение этих терминов обеспечивает постепенный переход к более свернутым суждениям при сравнении объемов понятий и лучшему осознанию понятий обобщения и конкретизации.

Как уже неоднократно подчеркивалось, при обучении обобщению и конкретизации важно, чтобы учащиеся смогли отличить свойства-следствия от свойств, независимых от других свойств (свойства, вытекающие из первичного содержания понятия, от свойств, входящих в него). Поэтому предлагаем такую задачу.

32. Указать несколько свойств параллелограмма, являющихся следствиями свойств, входящих в определение параллелограмма (вытекающих из свойств, входящих в определение).

Пусть при решении этой задачи выделены следующие свойства, принадлежащие производному содержанию понятия параллелограмма:

3) Имеется пара конгруэнтных сторон.

4) Имеется пара параллельных сторон.

5) Имеется центр симметрии.

В таком случае при решении последней задачи по существу решались каждый раз задачи на доказательство факта, что если свойства 1 и 2 выполняются, то и свойства 3-5 также выполняются.

Чтобы добиться от учащихся понимания, что включение в определение понятия следствий его первичного содержания не приводит к конкретизации понятия, предлагается такая задача.

33. Почему в определении параллелограмма не указываются все перечисленные свойства 1-5?

По форме данная задача не совпадает с традиционной. Решение этой задачи позволяет учащимся осознать, что включение в определение "лишних" свойств не приводит к новому понятию. Определение делается от этого громоздким и неудобным для использования в доказательствах. Если бы свойства 1-5 входили в определения параллелограмма, то для доказательства, что некоторый четырехугольник - параллелограмм, нужно было бы доказывать выполнение всех пяти свойств. Кроме того, в самом начале нужно было бы доказывать и непротиворечивость всех пяти свойств. Поэтому включение в определение свойства, являющегося следствием других включенных свойств, нецелесообразно. Осознание этого факта учащимися оказывает существенную помощь в повышении их математической культуры.

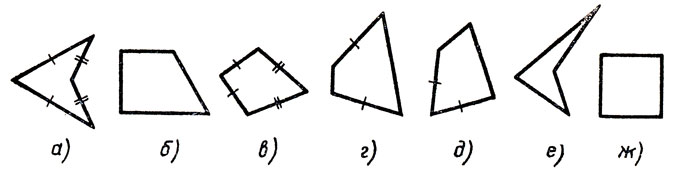
Рис. 3

Следующая задача подводит итог предыдущих задач.

34. A - множество четырехугольников, обладающих свойством 2; B - множество четырехугольников, обладающих свойствами 2-5. Изобразите эти множества с помощью диаграммы Эйлера. Какое из этих двух понятий есть обобщение (конкретизация) другого?

35. Какими из перечисленных свойств обладает каждый из четырехугольников, изображенных на рисунке 3?

Устанавливая выполнение или невыполнение свойств для фигур, изображенных на рисунке 3, учащиеся тем самым устанавливают неявно независимость одних свойств от других. Например, в случае а) выполняются свойства 1 и 3, а другие свойства не выполняются, потому что они независимы от свойств 1 и 3. В этом случае целесообразно поставить вопрос: можно ли свойства 2, 4, 5 доказать на основе свойств 1 и 3? Иначе: являются ли свойства 2, 4,5 следствиями 1 и 3? Случай ж) подчеркивает непротиворечивость свойств 1-5.

Предыдущая задача - по готовым чертежам. Более конструктивный характер носит следующая задача.

36. Изобразите четырехугольник, не являющийся параллелограммом и обладающий свойствами: а) 3; б) 4; в) 5; г) 3 и 4. Почему в случае в) искомого четырехугольника не существует?

Дайте другое определение параллелограмма, равносильное имеющемуся.

Важно, чтобы понятие непротиворечивости, независимости, необходимое и достаточное условие обобщения и конкретизации явно или неявно использовались при сравнении объемов понятий. Эту цель преследует следующая задача.

37. A - множество параллелограммов, B - множество четырехугольников, обладающих свойством 3; С - множество четырехугольников, обладающих свойством 4; E - множество четырехугольников, обладающих свойствами 3 и 4. а) Какое из этих множеств есть собственное подмножество какого-либо другого множества? б) Какое из этих понятий есть обобщение какого-либо другого понятия? в) Изобразите эти множества попарно с помощью диаграммы Эйлера, г) Является ли понятие четырехугольника, обладающего свойством 3, обобщением или конкретизацией понятия четырехугольника, обладающего свойством 4?

Предложенная задача - это также и задача на сравнение объемов понятий, ни одно из которых не является обобщением или конкретизацией другого (сравнение множеств B и C). Выяснение, не является ли одно из множеств B и C подмножеством другого, состоит ли из трех логически взаимосвязанных частей. При этом учащиеся осознанно используют понятие обобщения и конкретизации, представление о том, в каком случае одно понятие считается обобщением или конкретизацией другого. Приведя примеры объекта, принадлежащего пересечению множеств B и C (например, равнобедренная трапеция, параллелограмм), они делают вывод о том, что пересечение B и C непусто и, возможно, одно из двух понятий, о которых говорится в пункте г), есть обобщение другого. Установив, что трапеция, у которой нет конгруэнтных сторон, принадлежит множеству C и не принадлежит множеству B, ученик делает предположение, что C - более широкое множество, чем B т. е., возможно, B⊂C. Однако установление, что среди четырехугольников, имеющих пару конгруэнтных сторон, есть и такие, которые не имеют параллельных сторон (например, ромбоид, не являющийся ромбом) приводит к выводу, что ни одно из указанных в пункте г) понятий не является обобщением другого.

Только что подробно рассмотренная часть задачи представляет для учащихся значительные трудности. Поэтому в итоге ее решения должен появиться рисунок, наглядно раскрывающий полученный вывод. Он представляет собой диаграмму Эйлера, дополненную изображениями соответствующих четырехугольников (см. рис. 4). (Этот рисунок находится в соответствии с требованием об использовании конечных множеств при сравнении объемов понятий.)

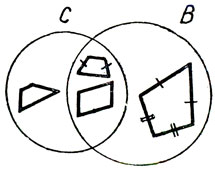
Рис. 4

В следующей задаче предлагается сравнить объемы понятий, ни одно из которых не есть обобщение другого.

38. Установите, не является ли одно из двух понятий: а) понятие четырехугольника, имеющего пару параллельных сторон и б) понятие четырехугольника, имеющего две пары конгруэнтных сторон - обобщением другого.

В результате решения должен появиться рисунок, аналогичный рисунку 4.

Особая ситуация для обучения обобщению и конкретизации возникает при изучении понятий прямоугольника и ромба. Это вызвано тем, что из соображений удобства использования этих понятий в их первичное содержание включены свойства - следствия других свойств. Например, для случая прямоугольника имеем следующие, содержащиеся в определении свойства.

1) Прямоугольник ABCD - параллелограмм.

2) A=90°; 3) B=90°; 4) C=90°; 5) D=90°.

Поэтому здесь после перечисления свойств, входящих в определение, с целью обучения обобщению и конкретизации целесообразно предложить следующие две задачи.

39. Коля, давая определение прямоугольника, опустил свойство 5. Будет ли определенная им фигура прямоугольником?

40. A - множество прямоугольников. B - множество параллелограммов, обладающих свойствами 2 и 3. C - множество параллелограммов, обладающих свойством 2. D - множество параллелограммов. Докажите, что B=C=A, A≠D, A⊂D. Какое определение можно дать прямоугольнику?

Обучение обобщению и конкретизации позволяет более целенаправленно, четко и последовательно организовать работу с учащимися по формированию и изучению понятий, обеспечить их более высокую математическую подготовку, развитие, умения и навыки самостоятельного изучения новых понятий.

Осуществление обучения обобщению и конкретизации при изучении понятий способствует систематизации традиционных задач и является также методом построения системы задач, в большей мере обеспечивающей успех работы по формированию понятий.

Необходимо иметь в виду, что в данном параграфе указаны различные возможности обучения обобщению и конкретизации. Использовать их следует при изучении всех разделов программы выборочно. При изучении одного и того же понятия не обязательно предлагать все типы задач; из них необходимо отобрать те, которые отвечают целям и задачам изучения понятия. Многие из предложенных выше задач могут быть опущены при первом изучении понятия и могут быть использованы для повторения материала. Кроме того, предложенные задачи преследуют цель раскрыть на конкретных примерах возможности обучения обобщению и конкретизации и тем самым показать учителю, как он может действовать при изучении других понятий.

Возможно также, что некоторые учителя сочтут возможным ввести более четко и явно термины "независимость", "непротиворечивость", "объем понятия". Это зависит от уровня подготовки учащихся, от мастерства учителя.