Обучение обобщению и конкретизации при изучении понятий в IV-V классах

Работа по обучению обобщению и конкретизации при изучении геометрических понятий в IV-V классах носит "неявный характер". Учащимся не сообщаются такие термины, как "обобщение", "конкретизация", "независимость", "непротиворечивость", "следствие". Вместо этих терминов используются выражения "это множество "шире", "это множество "уже", "это свойство может выполняться, а "это" свойство может в то же время не выполняться", "если "это" свойство выполнено, то "второе" не может выполняться", "если это свойство выполнено, то это не значит, что и "это" свойство выполняется", "эти два свойства одновременно не могут выполняться", "при выполнении "этого" свойства "другое" свойство может выполняться и может не выполняться". Учащиеся IV-V классов могут также пользоваться выражениями: "эти свойства противоречивы", "эти свойства непротиворечивы" в силу близкого к математическому смыслу вкладываемого в них "житейского смысла", известного учащимся. Однако эти выражения должны играть сопутствующую роль и раскрываться такими, как "эти свойства одновременно выполняться не могут", "если одно из этих свойств выполняется, то другое не выполняется", "эти свойства могут выполняться одновременно".

После введения понятия подмножества и отношения включения для множеств в V классе наряду с выражениями "это множество шире", "это множество уже" используются выражения: "это множество есть собственное подмножество "этого" множества", "это множество содержит в себе "вот это" множество" и соответствующая символическая запись.

Перейдем к рассмотрению задач, в процессе решения которых осуществляется обучение обобщению и конкретизации.

Прежде всего отметим, что в IV-V классах существенную "подготовительную" роль играют занимательные задачи и задачи, использующие материал алгебры. Приведем примеры таких задач.

1. Капризный Петя потребовал, чтобы ему купили собачку, обладающую одновременно двумя свойствами:

1) Вся собачка должна быть черной.

2) Вся собачка должна быть рыжей.

Может ли быть удовлетворен Петин каприз?

Решая эту задачу, учащиеся неявно знакомятся с понятием противоречивости свойств. Они говорят, что такой собачки не существует, что если собачка рыжая, так она не черная, а если черная, так не рыжая.

2. Существуют ли два таких числа a и b, для которых выполняются два таких свойства:

1) a/b=3; 2) ab=0.

Эта задача, как и предыдущая, - на установление противоречивости свойств.

3. Существуют ли два таких числа a и b, для которых выполняются два таких свойства:

1) a/b=2; 2) ab=2.

Выяснив, что такими числами могут быть числа 2 и 1, учащиеся неявно осознают непротиворечивость указанных свойств для чисел a и b. Следовательно, эта задача - на установление непротиворечивости свойств.

4. Коля сначала искал такие два натуральные числа a и b, для которых выполняются свойства: 1) ab=0; 2) число а на 1 больше числа b. Нашел ли он два таких числа? Найдет ли Коля два таких натуральных числа a и b, для которых выполняются указанные два свойства и еще одно свойство: 3) a+b=1. Какие это числа? Почему эти числа оказались теми же самыми?

Эта задача - на установление независимости свойств 1 и 2 и одновременно на выявление того, что свойство 3 есть следствие свойств 1 и 2. Учащиеся должны сделать вывод, что натуральные числа, обладающие свойствами 1 и 2, существуют (эти свойства могут выполняться одновременно), что свойство 3 обязательно выполняется, если выполняются свойства 1 и 2. В данной задаче неявно проводится мысль, что включение в множество свойств их следствия не приводит к конкретизации.

5. Найдите такие два натуральных числа m и n, для которых выполняются три свойства: 1) mn=0, 2) m меньше n на 2, 3) m+n=2. Затем найдите такие два натуральных числа m и n, для которых выполнены свойства 1 и 2. Почему получилось то же самое множество чисел, что и в первом случае?

Здесь учащиеся в неявной форме должны осознать, что если исключаемое свойство есть следствие "остающихся" свойств, то его исключение не приводит к обобщению. При решении этой задачи необходимо помочь учащимся понять, что если свойства 1 и 2 выполняются, то и свойство 3 обязательно выполняется - независимо от того, упоминается оно в задаче или нет. По этой причине во втором случае получаются те же самые значения m и n.

Задачи 4 и 5 можно отнести и к задачам на установление непротиворечивости свойств, и к задачам на усвоение необходимого и достаточного условия обобщения и конкретизации при исключении (включении) некоторого свойства, т. е. они выполняют не одну функцию.

Наличие задач 4 и 5 означает также выполнение требования об единстве обучения обобщению и конкретизации.

Рассмотрим далее задачи, опирающиеся на свойства биссектрисы угла (IV класс).

6. Пользуясь определением биссектрисы угла, перечислить ее свойства.

Очевидно, что данная задача относится к типу на перечисление свойств, входящих в определение (в первичное содержание понятия).

Эти свойства следующие:

1) Биссектриса угла - это луч.

2) Биссектриса угла выходит из вершины угла.

3) Биссектриса угла делит его пополам.

7. а) Откажемся от свойств 2 и 3 биссектрисы угла. Будем считать биссектрисой угла фигуру, удовлетворяющую свойству 1. Изобразите угол и несколько фигур, которые можно при этом условии считать биссектрисами изображенного угла. Сколько таких фигур можно построить?

(Учащийся должен понять, что в этом случае любой луч можно считать биссектрисой.)

б) Будем считать биссектрисой угла фигуру, удовлетворяющую свойствам 1 и 2. От свойства 3 откажемся. Изобразите несколько фигур, которые можно в этом случае считать биссектрисами угла. Сколько таких фигур можно построить? Всякий ли луч, выходящий из вершины угла, делит этот угол пополам?

в) Когда Коля учился в III классе, он спросил у старшего брата: "Что такое биссектриса?" Брат ответил ему: "Это луч, который делит угол пополам". Коля поверил ему. Изобразите угол и несколько фигур, которые Коля будет считать биссектрисами этого угла. Сколько будет у Коли биссектрис?

Обязательно ли выполняется свойство 2, если выполняются свойства 1 и 3?

г) Будем под биссектрисами угла подразумевать фигуру, удовлетворяющую свойствам 1, 2, 3. Изобразите биссектрису угла. Можно ли в определении биссектрисы угла опустить одно из свойств (получим ли тогда то же самое)? Какое множество шире: множество биссектрис или множество лучей, обладающих свойством 2; множество биссектрис или множество лучей, обладающих свойством 3? Почему?

Решая задачу 7, учащиеся должны осознать роль каждого из свойств, входящих в первичное содержание биссектрисы угла. Они начинают понимать, что "потеря" свойства может привести к другому понятию, объем которого будет представлять более широкое множество объектов. Данная задача выполняет функции нескольких типов: в ней устанавливается независимость свойств, вырабатывается представление о необходимом условии обобщения и конкретизации при исключении и включении некоторого свойства. В неявном виде здесь учащиеся встречаются с обобщением и конкретизацией, что означает выполнение требования о единстве в обучении этим мыслительным операциям. В процессе решения учащиеся изображают в данном случае некоторое конечное число объектов, которые принадлежат объему рассматриваемого понятия, сравнивают множества этих объектов. Следовательно, в этой задаче неявно устанавливается, не является ли одно из понятий обобщением другого, используются для получения и осмысления выводов конечные множества.

Большие возможности обучения обобщению и конкретизации содержит в себе изучение точечных отображений в V классе. Рассмотрим это для случая изучения параллельного переноса.

Прежде всего необходимо добиться овладения учащимися свойствами, перечисленными в учебнике при раскрытии содержания (первичного содержания) понятия "параллельный перенос фигур". Поэтому предлагаем следующую задачу.

8. Как перемещаются точки при параллельном переносе?

После выделения свойств необходимо записать (на доске и в тетрадях);

1) При параллельном переносе все точки перемещаются в одном и том же направлении.

2) При параллельном переносе все точки перемещаются на одно и то же расстояние.

На начальной стадии изучения параллельного переноса фигуры полезно воспользоваться конечными множествами точек. С этой точки зрения удобна модель, состоящая из 16 точек пересечения прямых, образующих сетку квадратов ("клетчатую бумагу") (см. рис. 2). Указанные точки пронумерованы и обозначены соответствующими цифрами (и сочетаниями цифр) от 1 до 16.

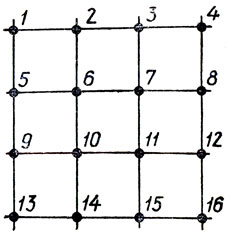
Рис. 2

На основе этой модели можно предложить ряд задач на обучение обобщению и конкретизации.

9. Фигура F = {1, 2, 3} перешла в фигуру Ф = {5, 10, 15} так, что точка 1 перешла в точку 5 (краткая запись 1→5), точка 2 отобразилась (перешла) на точку 10 (2→10), точка 3 отобразилась на точку 15 (3→15).

Выполняется ли здесь первое свойство параллельного переноса фигуры? второе свойство?

При решении данной задачи устанавливается независимость второго свойства параллельного переноса фигуры от первого свойства.

10. Фигура F = {2, 3} отобразилась (перешла) на фигуру Ф = {1,4}, причем точка 2 перешла в точку 1, а точка 3 - в точку 4. Выполняются ли свойства параллельного переноса фигуры в этом отображении F на Ф?

Решение этой задачи позволяет учащимся сделать вывод, что второе свойство параллельного переноса может быть выполнено, а первое свойство при этом может и не выполняться.

11. Фигуру F = {1, 2} отобразили на фигуру Ф = {3, 4} двумя способами: а) 1→4, 2→3; б) 1→3, 2→4. Которое из этих двух отображений есть параллельный перенос? Почему?

Данная задача подчеркивает непротиворечивость свойств параллельного переноса фигур.

12. Каким образом можно отобразить фигуру F = {2, 3} на фигуру Ф = {6, 7}? Сколько всего способов отображения F на Ф в данном случае? Сколько из них являются параллельным переносом? Почему параллельных переносов меньше, чем всех отображений?

Отвечая, что всех отображений первой фигуры на вторую два, а параллельный перенос один и что параллельных переносов меньше потому, что в одном отображении не выполняется первое свойство, а в параллельном переносе оно должно выполняться, учащиеся осознают, что дополнение второго свойства первым ведет к уменьшению количества отображений (т. е. к конкретизации).

Таким образом, приведенная задача вместе с задачами 10 и 11 образует "задачу" на уяснение необходимого и достаточного условия конкретизации понятия при включении в его первичное содержание нового свойства.

13. Коля сказал, что параллельный перенос - "это когда одна фигура переходит в другую так, что все точки первой фигуры перемещаются на одно и то же расстояние". Как вы оцениваете Колины знания? Какие из указанных отображений фигуры F = {6, 7, 11, 10} на фигуру Ф = (1, 4, 16, 13} можно считать на основании Колиного определения параллельным переносом: а) 6→1, 7→4, 11→16, 10→13; б) 6→4, 7→1, 11→13, 10→16; в) 6→1, 7→4, 11→13, 10→16. Можно ли первую фигуру отобразить на вторую с помощью параллельного переноса? Почему? Можно ли опустить первое свойство параллельного переноса фигур?

Эта задача выполняет несколько функций, отраженных в наименовании типов задач в первой части этого параграфа. Во-первых, в сочетании с задачей 10 она образует "задачу" на уяснение необходимого и достаточного условия обобщения понятия при исключении свойства из определения (из первичного содержания) понятия. Во- вторых, вместе с предшествующей задачей она способствует осуществлению требования о единстве обучения обобщению и конкретизаций. В-третьих, это и задача на установление противоречивости свойств: данные фигуры неконгруэнтны, что противоречит свойству параллельного переноса фигур - всякая фигура переходит в конгруэнтную ей фигуру; вследствие этого не существует параллельного переноса, отображающего первую фигуру на вторую.

14. Какие свойства параллельного переноса, кроме двух ранее указанных, вы знаете?

Эта задача - на выявление и перечисление свойств, входящих в производное содержание понятия (являющихся следствием первичного содержания).

Для удобства использования выявленных свойств в последующих задачах нужно эти свойства пронумеровать и записать. В данном случае выделим свойство 3: "При параллельном переносе всякая фигура переходит в конгруэнтную ей фигуру".

При решении задачи 13 это свойство было использовано для установления невозможности отобразить первую данную фигуру на вторую путем параллельного переноса. Этим самым подчеркивалось, что если свойства 1 и 2 выполняются, то и свойство 3 выполняется (т. е. оно есть следствие первых двух свойств).

15. Коля сказал, что параллельный перенос фигуры - это отображение одной фигуры на другую, в котором выполняются свойства 1 и 2. Саша сказал, что "это отображение, в котором выполняются свойства 1, 2 и 3". После этого им предложили фигуру F = {5, 1, 2} отобразить на фигуру Ф = {7, 3, 4} путем параллельного переноса. Коля получил: 5→7, 1→3, 2→4. Как отобразит точки 5, 1, 2 Саша? Почему он получил то же самое?

Предложенная задача способствует усвоению необходимого и достаточного условия конкретизации при включении в первичное содержание нового свойства.

Большую пользу приносят задачи на самостоятельное "конструирование" отображения одной фигуры на другую и на использование отношения включения множества. Например, можно предложить учащимся отобразить фигуру F = {2, 3, 7, 6} на фигуру Ф = {10, 11, 15, 14} так, чтобы: а) это отображение было параллельным переносом; б) не выполнялось второе свойство, а первое свойство выполнялось; в) свойство 1 не выполнялось, а свойство 2 выполнялось. A - множество отображений F на Ф в случае а); B - множество отображений F на Ф в случае б); C - множество отображений в случае в). Какое множество есть собственное подмножество других множеств? Какие отношения верны: A⊂B, A⊂C, B⊂A, C⊂A, B⊂C?

Успешное решение задач такого рода означает более высокий уровень неявного осознания учащимися понятия независимости свойств, их непротиворечивости, понимания отношения включения множеств.

Аналогичным образом может быть построена работа по обучению обобщению и конкретизации при изучении центральной симметрии.

Благодатным материалом для обучения обобщению и конкретизации является материал о смежных углах (IV класс). Здесь можно выделить следующие свойства, входящие в определение (первичное содержание) понятия смежных углов:

1) Смежных углов - два.

2) Объединение смежных углов - развернутый угол.

3) Пересечение смежных углов - луч.

В качестве свойства-следствия (свойства, принадлежащего производному содержанию понятия) можно выделить свойство:

4) Сумма величин смежных углов равна 180°.

Работу по обучению обобщению и конкретизации здесь можно строить аналогично тому, как это показано для случаев биссектрисы угла и параллельного переноса фигуры.

Для установления независимости свойств, входящих в первичное содержание понятия смежных углов, можно воспользоваться таблицей всевозможных случаев выполнения и невыполнения свойств 1-3. В таблице 1 выполнение свойства отмечено знаком "+", невыполнение - знаком "-". Ученик, выполнивший, к примеру, рисунок для случая 7, неявно убеждается в независимости третьего свойства от первых двух свойств. Переход от случая 5 к случаю 7 может быть использован для неявного осознания учащимися, что исключение из определения смежных углов свойства 3 ведет к обобщению понятия (расширению его объема). Сделав акцент на случае 7 и перейдя от него к случаю 5, мы подчеркнем конкретизирующую роль свойства 3. Чертеж для случая 5 показывает непротиворечивость свойств 1-3 смежных углов, показывает, другими словами, что смежные углы существуют. Установление, что не существует смежных углов, для которых выполняется свойство: "Сумма величин смежных углов не равна 180°", означает установление противоречивости этого свойства свойствам 1-3.

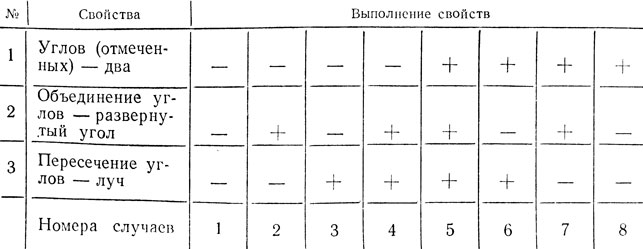
Таблица 1

Рассмотренные задачи показывают, что при изучении геометрических (и алгебраических) понятий в IV-V классах имеются широкие возможности для обучения учащихся обобщению и конкретизации.

Поступая аналогично, опираясь на сформулированные в первой части данного параграфа требования к обучению обобщению и конкретизации при изучении понятий, учитель сможет осуществить такое обучение и при изучении других понятий, здесь не рассмотренных.