Теоретико-множественная трактовка понятий "объем понятия" и "содержание понятия"

Объем понятия есть множество объектов, удовлетворяющих определению понятия; содержание понятия есть множество свойств, которыми обладает понятие.

1. Объем понятия может содержать конечное множество объектов. Например, объем понятия четного однозначного числа есть множество А = {2, 4, 6, 8}; объем понятия двузначного числа, кратного 3, есть множество В - {12, 15, 18, 21, 24, 27, 30, ..., 96, 99}. Если число объектов, входящих в объем понятия, невелико, то эти элементы в условиях обучения могут быть учащимися перечислены (как это сделано в случае указания множества А). Если же конечное число объектов, входящих в объем понятия, таково, что на их полное перечисление уйдет много времени, то обычно перечисляются не все объекты, а лишь некоторые - "первые" и "последние" (а иногда и некоторые "промежуточные", если в этом имеется необходимость). "Промежуточные" объекты, как это сделано при записи множества В, заменяются обычно многоточием (...).

Объем понятия может содержать бесконечное множество объектов. Примером могут служить объем понятия натурального числа, кратного 4, и объем понятия параллелограмма. Объем первого из этих понятий записывают обычно так: С = {4, 8, 12, 16, 20, 24, 28, 32, 36, ...}. В этой записи многоточие заменяет бесконечное множество натуральных чисел, кратных 4 и больших 36. Несколько иначе обстоит дело с объемом понятия параллелограмма. Множество объектов, входящих в объем понятия параллелограмма, несчетно, поэтому эти объекты не могут быть пронумерованы. Кроме того, в отличие от предыдущих примеров, неясно, в каком порядке их целесообразно перечислять. Поэтому в практике обучения выделение множества параллелограммов производится на неупорядоченном конечном множестве фигур. Например, на рисунке 1 изображено некоторое конечное множество фигур (множество М). Множество V параллелограммов, являющееся подмножеством, выделено на рисунке с помощью диаграммы Эйлера.

Однако, если параллелограммы из М обозначить P₁, P₂, P₃, то получим:

V = {P₁, P₂, P₃}.

А теперь сравним все рассмотренные примеры объемов понятий. У них есть общность: во всех случаях, чтобы создать представление об объеме того или иного понятия, мы, выбрав некоторое конечное подмножество бесконечного множества, выделяли из него новое (конечное) подмножество. В случае получения множества A мы из множества натуральных чисел выделяли подмножество однозначных натуральных чисел, а затем уже из этого множества - множество A. Множество B мы получали аналогично, причем в записи этого множества перечисляли (по нашему усмотрению) лишь элементы его некоторого подмножества. То же самое можно сказать о получении множества C: из множества N мы, возможно, не осознавая этого, выделили первые несколько десятков натуральных чисел (т. е. конечное подмножество), а из этого конечного подмножества выписали первые 9 чисел, кратных 4. В последнем случае из бесконечного множества фигур мы выделили конечное множество M, а из него - множество V параллелограммов.

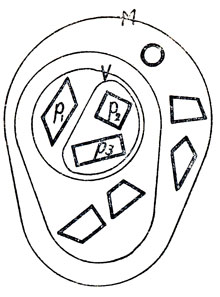
Рис. 1

Приведенные примеры показывают, что для того, чтобы дать учащимся представление об объеме понятия, в практике обучения широко используются задачи по выделению из некоторого конечного множества объектов подмножества, входящего в объем понятия. Решение такого рода задач является важным средством формирования правильных представлений об объеме того или иного понятия и используется при обучении обобщению и конкретизации.

2. Как и объем понятия, содержание понятия может представлять собой бесконечное множество свойств. Однако роль этих свойств при формировании понятия и при его использовании в процессе решения задач различна. Одни из них входят в определение понятия, другие являются их следствиями. Дополнение свойств, входящих в определение, их следствиями не меняет объема понятия, приводя лишь к так называемому "избыточному" определению. Таким образом, можно сказать, что содержание понятия "определяется" множеством свойств, входящих в определение. При введении понятия первоначально под его содержанием учащимися мыслится именно это множество. Множество свойств, входящих в определение понятия, будем называть поэтому первичным содержанием понятия. Множество свойств, являющихся следствием первичного содержания, назовем производным содержанием понятия. Следовательно, содержание понятия в принятой терминологии представляет собой объединение первичного и производного содержаний.

В качестве примера рассмотрим понятие параллелограмма. Его первичное содержание представляет собой множество, состоящее из свойств a₁ и a₂, где a₁ и a₂ - следующие:

a₁. Параллелограмм - это четырехугольник.

a₂. Противоположные стороны параллелограмма параллельны.

В производное содержание понятия параллелограмма входят такие свойства, как b₁-b₄.

b₁. Противоположные стороны параллелограмма конгруэнтны.

b₂. Диагонали параллелограмма точкой их пересечения делятся пополам.

b₃. Точка пересечения диагоналей параллелограмма есть его центр симметрии.

b₄. Не во всякий параллелограмм можно вписать окружность.

Первичное содержание понятия параллелограмма α = {a₁, a₂). Множество β = {b₁, b₂, b₃, b₄} есть подмножество его производного содержания γ:

β⊂γ

Такие подмножества дают представление о производном содержании понятия. Содержание φ понятия параллелограмма может быть представлено тогда как объединение множеств α и γ:

φ = α ∪ γ

Выяснение, принадлежит ли некоторое свойство производному содержанию понятия, поиски свойств, входящих в производное содержание понятия, с целью их использования в системе задач, являются важными элементами в обучении обобщению и конкретизации.