Использование свойств функций при решении уравнений и неравенств (Бокарева Т.А.) (Таганрогский муниципальный общеобразовательный лицей при ТРТУ) (УДК 37. 047)

(Дается методическая разработка занятия по указанной теме.)

Нередко бывает, что при решении уравнений ƒ(x)=g(x) или неравенств f(x)≤g(x) преобразование или замена переменной не упрощают и не приводят их к стандартным уравнениям и неравенствам. В таких случая иногда полезно использовать некоторые свойства функций ƒ(х) и g(x). Рассмотрим следующие ситуации.

1. Использование монотонности функций на промежутке позволь решать такие уравнения как log₃(x-3)=2^6-x. На области определения уравнения х∈(3;+∞) функция у=log₃(x-3) возрастает, а функция у=2^6-х убывает. Корень уравнения можно найти подбором: х=6. Он является единственным.

Решим неравенство

Так как область определения неравенства задается неравенством x<8, то прологарифмировав обе части неравенства по основанию 2, получим равносильное ему неравенство

Равенство log₂³(8-x)=3x-4 выполняется при х=4. Поскольку функция y=log₂³(8-x) убывает, а функция у=3х-4 возрастает, то неравенство log₂³(8-х)≤3х-4 выполняется при х≥4. Итак, 4≤х<8 - решение исходного неравенства.

2 Часто графическое решение уравнения или неравенства приводит более наглядному результату. Например, при решении иррационального уравнения √7-x=x-l, построив графики функций y=√7-x и у=х-1, находим единственный корень х=3.

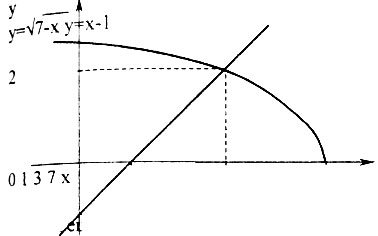
Решая неравенство √х+2>х таким способом, получаем что, х∈(-2;2) является решением данного неравенства.

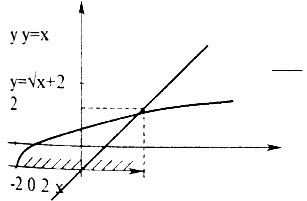
3. Если функция ƒ(х) на промежутке I ограничена сверху, причем supx∈Iƒ(x)=A, а функция g(x) ограничена снизу и infx∈Ig(x)=A, то уравнениеƒ(х)=g(x) равносильно системе уравнений

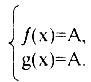
Решим уравнение 3^|х|-cos²x/3. Поскольку cos²x/3≤l и 3^|х|≥1 для любого действительного х, то данное уравнение равносильно системе уравнений

которая имеет единственное решение х=0. Следовательно, х=0 - единственный корень исходного уравнения.

4. Используются и другие элементарные приемы решения, например с привлечением производной.

Исследуем уравнение ƒ(х)-ƒ(1/(х+1 ))=а, где ƒ(х)=х+1/(х+1). Для этого рассмотрим функцию φ=ƒ(х)-ƒ(1/(х+1)) и построим ее график.

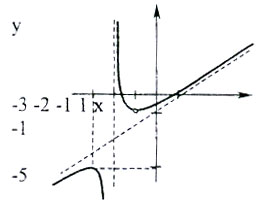
Итак, φ(х)=х-(х+1)/(х+2), х≠-1, х≠-2. В результате, множество значений функции у=φ(х): у≤-5, у>-1. Отсюда делаем вывод, что уравнение решений не имеет при а∈(-5;-1]; имеет единственное решение при а=-5; имеет два решения при а∈(-∞;-5)∪(-1;+∞).

Решим неравенство х⁹+х⁶+448<0. Для этого исследуем функцию y=x⁹+x⁶+448 И построим ее график.

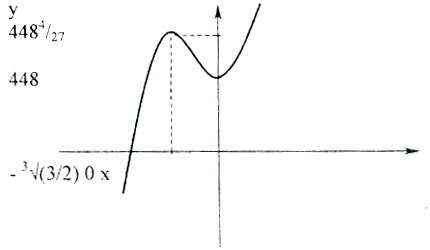
Равенство х⁹+х⁶+448=0 выполняется для одного х, причем х<0. Подбором находим корень: х=-2. Следовательно, решение неравенства задается х<-2.

Следует отметить, что подобные задачи встречаются как на выпускных школьных экзаменах, так и на вступительных экзаменах в вузы. Например, в варианте А-11 (№2-98) экзаменационной работы по алгебре началам анализа было предложено решить уравнение log2(x²-4x+8)=sin(5πx/4)-cos(πx/2), которое можно исследовать, пользуясь описанными выше методами. На вступительных экзаменах в ТРТУ предлагались такие задачи как

• Может ли принимать функция у=2х²-4х+0, 5-ln(х-1) отрицательные значения? (1994г.)
• Выписать в ответ то из уравнений (если такое есть), которое не имеет решений: arccos х=π/7; sin x=(-3+√21)/2; ln х²=1; 2^х2=1/6. (1996г.)
• Показать, что уравнение √x+√x-16=2sin89° не имеет решений. (1992г.)

Таким образом, при повторении всего курса алгебры и начал анализа следует уделить внимание подобным задачам. Это позволит повторить и систематизировать свойства функций, отработать умение учащихся пользоваться ими для решения уравнений и неравенств.