Об активных формах повторения программы по математике (Иванов Е.А., Иванова В.М., Костенко Т.В.) (Таганрогский муниципальный общеобразовательный лицей при ТРТУ, Таганрогская муниципальная средняя школа № 8) (УДК 378.146:51)

(Настоящее сообщение посвящено обзору тестовых форм контроля и обучения, которые являются составной частью дидактико-методического комплекса, построенного на базе вариантов вступительных экзаменов по математике в ТРТУ.)

Одной из важных активных форм повторения в период окончательной систематизации школьного курса элементарной математики служат всевозможные тестовые виды контроля и самоконтроля выпускников. Они позволяют за короткое время охватить большое количество разделов программы и широкий круг обучаемых, определить порог знаний и уровень притязаний каждого абитуриента, выявить и устранить их типичные ошибки, являющиеся признаком формального усвоения тех или иных пунктов программы. Наряду с указанным выше, эти типы контроля выполняют и адаптационную функцию для абитуриентов - современные аттестационные технологии активно используют тесты, тестовые задания, задания тестовой форме, которые требуют полного и мобильного владения всем школьным материалом. Подготовка к их выполнению должна содержать специально разработанные приёмы для развития изобретательности, повышения скорости выполнения работы, умения мгновенно переключаться на различные типы заданий, повышения психологической устойчивости абитуриента. Разумеется, тесты используются в сочетании с другими способами повторения курса и подготовки к экзаменам и не могут их заменить, их роль прежде всего в обеспечении стандартной составляющей математического "багажа" абитуриентов.

Как показывает опыт авторов, работающих в различных учебных заведениях, наибольшую эффективность эти формы показывают при выявлении и искоренении типичных ошибок обучаемых. Выделим две основав такие формы.

1. Система утверждений, которая служит для определения уровня знания основных понятий, фактов, теорем программы по математике. Абитуриент за определённое время (10-15 минут на 20-25 задач), не пользуясь справочниками, определяет истинность или ложность заданных утверждений, составляя таблицу из "+" и "-" соответственно (например, "Область определения функции у = √-х - только х = 0"; "Квадрат - частный случай ромба" и т. п.). Преподаватель по истечении указанного времени приводит правильные ответы, кратко их комментируя, а контролируемые фиксируют число правильных ответов, обращая внимание на свои ошибки. Результаты тестирования могут сигнализировать учащемуся о пробелах в знаниях, о формальном усвоении формул и теорем, иногда о неумении оперативно распоряжаться известной информацией. Эта форма может использоваться как для контроля, так и для самоконтроля. Она допускает обобщения и усложнения как в сторону закрытых тестов (с выбором одного, а лучше комбинации правильных ответов, например, "число (√5 - √6)(√5+√6)√2 а) рациональное; б) иррациональное; в) положительное; г) отрицательное; д) равно 0"), так и открытых (например, "выписать в ответ продолжение теоремы синусов для 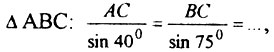, а также наибольшую из его сторон").

2. Система утверждений, обязательно содержащих неточности, логически неверные выводы, прямые ошибки. Абитуриент, зная заранее ложность приведенных утверждений, должен их проанализировать, найти и исправить ошибки (за достаточное, но не избыточное время), а затем сравнить свои исправления с приведенными после теста ответами. Преподаватель принимает более активное участие в обсуждении аргументации обучаемых, чем в предыдущем случае. При составлении таких тестов обязательно используются типичные ошибки абитуриентов (например, "Из того, что 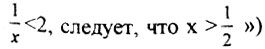") а также фрагменты задач экзаменов. Таким образом, тесты, кроме, контролирующего, носят и обучающий характер.

Приведем пример обучающего теста-кольца по выявлению и устранению типичных ошибок типа "Игнорирование области определения функции". Он представляет собой последовательность простых открытых тестов, связанных общей идеей; обучаемый, допустив ошибку (ошибки) при выполнении первых из них, как правило, самостоятельно осознает ее (их) при выполнении последующих и, возвращаясь, исправляет. Последний тест еще раз подчеркивает основную идею на более сложном примере: "Упростить выражение 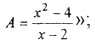"; "Построить график функции 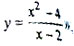"; "Найти область определения функции 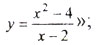"; "Решить уравнение 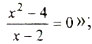"; "Упростить выражение А = tgx·ctgx и построить график функции у = tgx·ctgx".