II. Проблемы содержания, методики преподавания и контроля качества дисциплин естественно-научного цикла

К проблеме содержания математического образования в школах III ступени естественно-научного профиля (Иванов Е.А., Ольховой А.Ф., Орехов Б.И.) (Таганрогский муниципальный общеобразовательный лицей при ТРТУ) (УДК 371.3)

(Рассматриваются вопросы содержания математического образования в школах III ступени естественно-научного профиля. Предлагается вариант содержания курса алгебры и начал анализа.)

Реализация одной из основных целей общеобразовательного учреждения - создание основы для осознанного выбора и последующего освоения профессиональных образовательных программ - привела к появлению большого числа разнообразных профильных классов, работающих по различным учебным планам и программам.

На наш взгляд, профильное обучение и конкурсный отбор целесообразны и оправданы только для школ III ступени. К этому моменту у учащегося более или менее уже сформировалась система склонностей и приоритетов. Что касается школ I и II ступени, то здесь профильность и конкурсный отбор просто недопустимы, так как могут привести и приводят к психологическим травмам и неоправданным потерям "Эйнштейнов" для общества.

Анализ содержания математического образования учащихся III ступени выявляет его чрезмерное профилирование: физико-математическое, химико-биологическое, технологическое, экономическое, экологическое, гуманитарное и пр. Как следует из названия настоящей статьи, авторы являются противниками дифференциации содержания математического образования по таким профилям. Мы считаем, что содержание математического образования должно дифференцироваться по двум профилям - естестественно-научный (с направлениями: физико-математическое, химико-биологическое, технологическое, экономическое), гуманитарный (с направлениями: историческое, филологическое и др. ), с возрождением утерянных в большинстве школ, особенно городских, непрофильных классов с полноценным разносторонним общим образованием. Увлечение массовым профилированием, приводящее к исчезновению непрофильных классов, наносит ущерб общему образованию, приводит к нарушению прав ребенка на среднее полное образование и свободный выбор профессии в будущем.

Единый подход к проблеме содержания математического образования в классах естественно-научного профиля обусловлен следующим. Современная математика, может быть, самая совершенная и самая абстрактная область человеческой культуры. В то же время математика используется для решения разнообразных задач от повседневной жизни до вершин теоретической физики, биологии и инженерной практики. Эта двуединость, которую Эйнштейн назвал "внутренним совершенством и внешним оправданием", по сути может быть предъявлена к любым видам интеллектуальной практики человечества.

Внутреннее совершенство математики выражается в ее

• архитектонике, т. е. особого рода иерархической структуре ее понятий и предположений;
• методе, суть которого - формально-логическое доказательство;
• высокой степени абстрактности моделях, конструкциях и методах их обобщений.

С точки зрения внешнего оправдания, математика занимает особое место в человеческой культуре. С одной стороны, математика - это культуральный троп, т. е. один из способов человеческого понимания мира, в основе которого лежит иерархия формально-логических рассуждений, исходящих из конечного числа явных утверждений, исходных посылок и герметических по отношению к ним выводов. Такая структура математики позволяет для достаточно обширной области рассуждений показать их непротиворечивость, очертить круг проблем и более или менее четко поставить задачи в рамках решения этих проблем, что позволяет говорить о аподиктической достоверности математики.

С другой стороны, математика является языком науки, позволяющим - строить адекватные модели природных и общественных явлений вне зависимости от иерархии парадигм в конкретных областях знания. Таким образом, математика является естественной основой и мощным методом любой науки. Более того, математика формирует рационалистический склад ума, который, как писал Прокл Диодох в V веке нашей эры, "только и позволяет увидеть единство в многообразии, неделимое в делимом и бесконечное в конечном". Таким образом, все изложенное выше, общенаучные и общекультурные, а также гуманитарные аспекты этой науки определяют те общеизвестные цели и задачи обучения математике в школе, которые находят своё отражение во всех программах по математике^* и делают ее важнейшей частью естественно-научного комплекса дисциплин в школе

^* (Программы для общеобразовательных учреждений. Математика. М. , изд. "Просвещение", 1996 г. )

Прежде чем перейти к содержанию курса математики, отметим принципы, на которых должно основываться, как нам представляется, математическое образование в классах естественно-научного профиля^*

^* (Е. А. Иванов, Б. И. Орехов, А. Ф. Ольховой. К вопросу о содержании математического образования учащихся III ступени естественно-научного профиля. Тезисы докладов научно-методической конференции ВУЗов Северо-Кавказского региона "Технический университет в системе непрерывной профессиональной подготовки как центр науки, культуры и образования", Новочеркасск, изд. НГТУ, стр. 223-224., 1997 г.)

• Мы рассматриваем математическое образование на первых двух ступенях как пропедевтическое со всеми естественными целями и задачами.
• Математическое образование на Ш ступени должно носить относительно самостоятельный характер и не являться прямым продолжением предыдущего.
• Курс математики должен строиться на строгой логической основе и по возможности не содержать бездоказательных утверждений. Привлекая эвристику, необходимо проводить четкое различие между доказательствами и правдоподобными рассуждениями, ограничиваясь разумными мерами строгости. В курсе обязательно должно быть найдено место для обсуждения предмета математики вообще и её взаимодействий с действительностью.
• Центральные, стержневые понятия курса, такие, как множество элементы логики, функциональная зависимость, аксиоматический метод, должны быть достаточно подробно объяснены с максимальной степенью конкретности и наглядности.

Касаясь учебных планов классов естественно-научного профиля на III ступени обучения, отметим, что на математику в них должно отводится в 10-11 классах 8 часов в неделю, в том числе, 6 часов на алгебру и на чала анализа и 2 часа на геометрию. Таким образом, из числа двенадцать часов, отводимых базисным учебным планом на обязательные занятия занятия по выбору учащихся, мы на курс математики предлагаем взять пять часов, оставляя тем самым возможность реализовать вариативности учебных планов различных направлений естественно-научного профиля. При этом физико-математическое направление, оставаясь в рамках единого математического содержания данного профиля, должно использовать определённую часть часов учебного плана для осуществления уровневой дифференциации в обучении. Это означает, что следует не стремиться к расширению содержания, а направить усилия на развитие общей математической культуры и хорошей техники. Нам представляется целесообразным следующее распределение часов по видам занятий: лекции - 1 час, семинарские занятия - 1 час, практические занятия - 4 часа. Именно такой расчасовки мы придерживаемся в течение ряда лет в нашем лицее.

Главной особенностью лекционного курса математики, читаемого в лицее при ТРТУ, является его логическая выверенность: все основные предложения приводятся школьникам с доказательствами. Демонстрируя доказательства, лектор подчёркивает не только их внутреннюю логическую структуру, но и связь с другими теоремами курса. В результате школьники видят разворачивающуюся перед ними картину сотворения здания математики, проникаются её духом, начинают приобретать математическое сознание. Таким образом, помимо естественной прагматической цели дать школьнику в систематизированном виде знания, достаточные для поступления в ВУЗ, лекционный курс решает ещё и сверхзадачу - придаёт этим зданиям смысл, выходящий за рамки голого эмпиризма.

Однако логика как в математике, так и в других науках "не столько содействует исследованию того, что нам неизвестно, сколько позволяет излагать для других то, что мы уже знаем". Как же всё-таки научиться решать задачи? В лицее помимо лекций по математике проводятся ещё практические и семинарские занятия. Если на практических занятиях школьников учат владеть более или менее стандартными алгоритмами решения задач, то семинарские занятия играют двоякую роль: во первых, они служат для подкрепления на практике той части лекционного курса, которая не покрывается темами практических занятий (например, элементы матлогики, теории множеств, некоторые разделы высшей математики), во-вторых, семинары призваны научить подходам к решению задач повышенной сложности, вплоть до олимпиадных, то есть научить школьника поведению в условиях нестандартной математической ситуации и дать ему уверенность в том, что он с ней справится. На семинарах школьники практически осваивают способы исследования и получения того, что им неизвестно.

Примерное содержание обучения (курс алгебры и начал анализа).

1. Понятие о предмете математики и её методах.

Математика как наука о способах построения и исследования моделей. Аксиомы геометрии. Утверждение, отрицание утверждения. Формально-логический метод доказательства математических утверждений. Закон исключенного третьего, доказательство от "противного". Индукция, дедукция. Полная и неполная индукция. Метод математической индукции.

2. Элементы теории множеств.

Понятие множества в математике, примеры множеств, способы задания. Операции над множествами (объединение, пересечение, дополнение) их свойства (коммуникативность, ассоциативность, теоремы Де Моргана). Диаграммы Эйлера-Венна.

3. Элементы комбинаторики.

Упорядоченные множества, перестановки, число перестановок. Упорядоченные множества и размещения. Сочетания, число подмножеств конечного множества, свойства числа сочетаний, рекуррентная формула для вычисления числа сочетаний. Бином Ньютона.

4. Числовые множества.

Прямая и обратная теоремы, понятие о необходимых и достаточных условиях в математике. Число и цифра, понятие о позиционных система счисления, примеры. Множество натуральных чисел, делимость, свойства делимости. Необходимые и достаточные условия делимости на 2, 3, 4,5 9, 10. Основная теорема арифметики. Множество рациональных чисел Q, решение уравнения х²=2 на Q. Десятичная форма записи рациональных чисел, иррациональные числа. Рациональные приближения по недостатку и избытку. Множество действительных чисел. Понятие об операциях над действительными числами. Числовая прямая. Понятие полноты числовой прямой.

5. Бинарные соответствия и отношения. Декартово произведение множеств, примеры. Бинарные соответствия и oтношения, примеры. Геометрические иллюстрации, граф, график. Композиция отношений, примеры. Обратное отношение, примеры.

6. Числовые функции числового аргумента.

Постоянные и переменные величины. Независимые и зависимые переменные. Определение функции, область определения, множество значении Способы задания функций. График функции. Общие свойства функций чётность, нечётность, монотонность, ограниченность, периодичность. Простейшие функции, их свойства, графики: y=ax+b, у=|х|, у=[х], у={х}, y=sigх, у=а/х. Простейшие преобразования функций: сжатие, растяжение, сдвиги вдоль координатных осей. Функции y=(ax+b)/(cx+d), у=ах²+bх+с. Функция, обратная данной, определение, простейшие примеры, достаточное условие существования обратной функции, функция обратная к монотонно! Свойство графиков взаимно обратных функций.

7. Преобразование выражений на заданных множествах.

Преобразование алгебраических выражений на областях допустимых значений букв. Тождества и уравнения. Преобразование-следствие, равносильные преобразования и их приложение к решению уравнений и неравенств. Уравнения, неравенства и системы с параметрами.

8. Предел числовой последовательности.

Числовая последовательность, примеры. Способы задания, график. Арифметическая и геометрическая прогрессии. Ограниченная и бесконечная малая последовательности и их графики. Свойства бесконечно малых последовательностей. Сходящаяся последовательность, необходимое условий сходимости (формулировка). Число е. Действительные числа, как предел сходящихся последовательностей рациональных чисел. Операции над действительными числами.

9 Предел функции, непрерывность, дифференцируемость. еделение предела функции по Гейне. Свойства функций, имеющих предел в точке. Односторонние пределы, связь с двусторонним. Непрерывность функции в точке. Свойства функций непрерывных в точке. Теорема о сохранении знака, метод интервалов. Критерии непрерывности функции в точке. Примеры разрывных функций. Задачи, приводящие к понятию производной в точке. Определение производной, её физический и геометрический смыслы. Связь понятий "непрерывность" и "дифференцируемость". Уравнение касательной к графику функции. Основные правила вычисления производных. Производная сложной функции, производная обратной функции.

10. Степенная функция. Степенная функция с натуральным показателем, свойства, графики для случая чётного и нечётного показателей. Функция 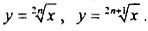. Степенная функция 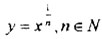и её свойства. Степенная функция 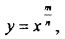её свойства. Тождественные преобразования выражений, содержащих степени. Решение иррациональных уравнений и неравенств. Степенная функция с действительным показателем и её свойства. Производная степенной функции.

11. Показательная и логарифмическая функции. Определение показательной функции, свойства и график. Производная показательной функции. Логарифмическая функция как обратная к показательной, свойства, график, производная. Логарифм числа. Арифметические свойства логарифмов. Десятичные и натуральные логарифмы. Тождественные преобразования выражений, содержащих логарифмы. Методы решения показательных, логарифмических уравнений и неравенств.

12. Тригонометрические функции.

Радианное измерение угловых величин. Длина дуги и площадь сектора. Функция y=sin х и её свойства, график. Функция y=arcsin х и её свойства, график. Решение уравнений вида sin х=а. Функция y=cos х и её свойства, график. Функция y=arccos х и её свойства, график. Решение уравнений вида cos x=a. Функция y=tg x и её свойства, график. Функция y=arctg х и её свойства, график. Решение уравнений вида tg х=а. Гармонические колебания.

13. Теоремы сложения и следствия из них.

Преобразование поворота на вектора угол α. Теоремы слоения для тригонометрических функций. Формулы привидения. Тригонометрические функции половинного и двойного аргументов, формулы понижения степени Преобразование суммы тригонометрических функций в произведение и наоборот. Тождественные преобразования тригонометрических выражений. Методы решения тригонометрических уравнений.

14. Комплексные числа. Многочлены в комплексной области.

15. Комплексные числа как упорядоченные пары вещественных чисел. Изображение комплексных чисел на плоскости. Алгебраическая форма записи комплексного числа. Операции над комплексными числами. Модуль и аргумент комплексного числа. Тригонометрическая форма записи комплексного числа. Формула Муавра. Решение уравнений zⁿ=a. Многочлен в комплексной области, операции над многочленами. Корень многочлена, делимость, теорема Безу. Схема Горнера. Формулировка основной теоремы алгебры. Свойства многочленов с действительными коэффициентами. Формулировка теоремы Абеля о разрешимости уравнений в радикалах.

16. Исследование функций и построение графиков.

Таблица производных основных элементарных функций. Возрастание и убывание функции. Критические точки функции. Необходимое и достаточное условие экстремума. Исследование функций и построение графиков. Наибольшее и наименьшее значение функции; приложения к решения конкретных задач. Производная второго порядка и её физический смысл Применение производных в физике и технике. Приближенные вычислена с помощью производной.

17. Первообразная и определённый интеграл.

18. Первообразная, основные свойства и правила нахождения первообразной Таблица первообразных. Задачи, приводящие к понятию определённого интеграла. Определённый интеграл. Формула Ньютона-Лейбница. Геометрические и физические приложения определённого интеграла.

Уровень и глубина проработки предложенного содержания обучения естественным образом должны дифференцироваться по направлениям в рамках рассматриваемого профиля. Содержание курса геометрии в указанные выше часы может быть изложено в рамках традиционных программы^*.

^* (Программы для общеобразовательных учреждений. Математика. М. , изд. "Просвещение", 1996 г.)

В заключение заметим, что в непрофильных классах III ступени на курс математики следовало бы отвести 6 часов в неделю, внеся соответствующие изменения в предложенную выше программу. Что касается классов гуманитарного профиля, то нам представляется неоправданна имеющееся сейчас резкое уменьшение числа часов на метематику. Дело в том, что роль математики не изменилась со времён Р. Декарта, который писал: "Математика приучает нас к познанию истины, поскольку в ней содержатся точные рассуждения, которые не встречаются нигде за её пределами. А поэтому тот, кто приучит свой ум и к математическим рассуждениям, сделает его также способным к исследованию других истин: ведь способ рассуждения всюду один и тот же". Таким образом, одна из главных задач курса математики заключается в воспитании у слушателей рационального, дискурсивного склада ума. Впрочем, это восходит к древним грекам - математика по-гречески и означает "воспитание знанием, полученным путём рассуждений".

Разумеется, в воспитании стиля мышления гуманитариев имеются свои особенности, которые обязательно необходимо учитывать при отборе материала и способе его изложения. Эти особенности, на наш взгляд, должны вытекать из трёх основных принципов:

1. Отказ от излишней утилитарно-технической ориентации курса, бездумной алгоритмизации методов решения конкретных задач.

2. Усиление логического компонента курса. Здесь следует, во-первых, подбирать задачи и упражнения, развивающие логическое, дискурсивное и творческое мышление, иллюстрирующие те или иные приёмы, принципы и методы доказательных рассуждений; во-вторых, обращать внимание на технику заведомо неправильных рассуждений (общую и математическую софистику), учить находить ошибки в чужих рассуждениях.

3. Активное привлечение исторического и познавательного материала. Здесь сведения из истории математики, биографии математиков, роль и значение тех или иных теорем в математике.

Впрочем, это является предметом отдельной статьи.