Равновесие тела с одyой или двумя закрепленными точками

Необходимо все время подчеркивать, что все то, что рассказывается в курсе статики, справедливо для абсолютно твердого тела. При рассмотрении различных систем сил: сходящейся, плоской, пространственной и т. д. надо каждый раз напоминать, что речь идет о различных системах сил, приложенных к абсолютно твердому телу. Иначе раздел, посвященный равновесию тела с одной и с двумя закрепленными точками, выглядит как искусственная вставка в курс. Речь шла о приведении к простейшему виду и о равновесии различных систем сил, а затем вдруг речь почему-то пошла о равновесии тела.

Когда на экзамене просишь студента написать уравнения равновесия для совершенно свободного твердого тела, то он, как правило, ничего не пишет. Если вы попросите написать уравнения равновесия для произвольной пространственной системы сил, то вам сразу напишут шесть уравнений равновесия. Это говорит о том, что студенты забывают, что в статике речь идет о приведении к простейшему виду и о равновесии различных систем сил, действующих на абсолютно твердое тело. Следовательно, тем чаще надо это повторять, чтобы студенты правильно все усвоили.

Очень много неприятностей на экзаменах бывает с разделом "Равновесие тела с одной и с двумя закрепленными точками". Этот простой раздел понимается и усваивается студентами плохо. Причина указана выше. Видимо, лучше всего его рассказывать, опираясь на понятие степеней свободы.

Совершенно свободное тело имеет шесть степеней свободы. Оно может как угодно двигаться поступательно и как угодно вращаться. Это произвольное поступательное движение можно разложить на перемещения по осям координат х, у, z (три степени свободы), а произвольное вращение можно разложить на вращения вокруг тех же координатных осей (еще три степени свободы).

Вот почему для равновесия совершенно свободного тела, на которое действует пространственная произвольная система сил, необходимо и достаточно, чтобы выполнялись шесть уравнений равновесия. Если тело закреплено в одной точке, то оно имеет три степени свободы. Двигаться поступательно такое тело не может, а может только вращаться вокруг любой оси, т. е. вокруг осей координат. Для того чтобы такое тело находилось в равновесии, нужно, чтобы оно не вращалось, а для этого достаточно потребовать равенства нулю трех уравнений моментов

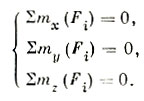
Итак, для того чтобы абсолютно твердое тело с одной закрепленной точкой, на которое действует произвольная пространственная система сил, находилось в равновесии, необходимо и достаточно, чтобы суммы моментов всех сил относительно трех взаимно перпендикулярных осей равнялись нулю.

Будут ли выполняться три других уравнения? Конечно. Они служат для определения составляющих реакции шарнира в точке крепления N_x, N_y, N_z (рис. 23). Эти уравнения записываются так

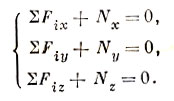
Тело, имеющее две закрепленные точки, имеет одну степень свободы. Оно может вращаться только вокруг оси, проходящей через эти две закрепленные точки (рис. 24). Равновесие будет в том случае, если тело не будет вращаться вокруг этой оси. Поэтому для равновесия достаточно потребовать, чтобы сумма моментов всех сил, действующих на тело, относительно оси, проходящей через две закрепленные точки, равнялась нулю: ∑m_xx(F_i)=0. Пять остальных уравнений служат для определения реакций в опорах. Здесь сразу же очень удобно переходить к понятию статически неопределенных задач в теоретической механике.

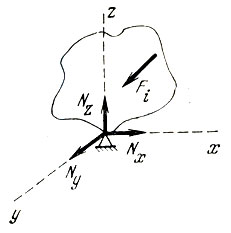
Рис. 23

Вначале студенты очень плохо представляют себе задачи по пространственной статике. Поэтому первое время можно рисовать пространственную задачу в трех проекциях.

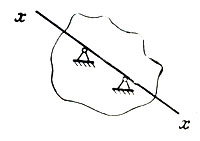
Рис. 24