Равновесие плоской произвольной системы сил

После главы о паре и обоснованной основной теоремы статики идет глава "Равновесие плоской системы сил".

В плоской статике лучше не рассматривать момент силы как вектор.

Рассказывая о приведении сил к центру, вместо "главный вектор" и "главный момент" С. А. Чаплыгин предлагает говорить "результирующий вектор" и "результирующий момент", так как точка приведения произвольная. Если мы говорим "главный вектор" и "главный момент" при приведении плоской системы сил к произвольной точке, то отсюда следует, что все векторы главные. Особенно это плохо для момента, который не инвариантен.

Когда о приведении плоской системы сил к произвольно выбранной точке рассказано, можно попробовать дать студентам такой пример. Имеется твердое тело, в точках которого А, В, С и D действуют силы F₁, F₂, F₃ и F₄ (рис. 19). К чему можно привести такую систему сил?

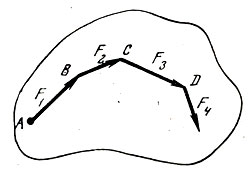
Рис. 19

Я неоднократно задавал своим слушателям такой вопрос на зачетах, экзаменах и, как правило, получал следующий ответ. Большинство студентов "замыкало" многоугольник, а не приводило его к точке. Вот почему надо всегда говорить "векторный", а не "силовой" многоугольник. Многоугольники первых глав образованы не силами, а векторами, их изображающими, т. е. силы не трогают, а изображающие их векторы можно переносить и строить где угодно, и результирующий вектор - это не силовой, а векторный многоугольник.

Говоря об особенностях приведения, надо указать четыре частных случая приведения: 1) П≠0, М≠0 2) П≠0, М=0; 3)П=0, М≠0; 4)П=0, М=0.

Только во втором случае результирующий вектор является равнодействующей. Подчеркнуть, что эти четыре случая получаются, если точка приведения произвольная, а к чему можно свести - это другое дело. Поэтому нельзя ставить вопрос: к чему приводится система сил/ Если ставится такой вопрос, то надо оговаривать - при произвольной точке, или иначе ставить вопрос: к чему можно привести систему сил для определенно выбранной точки?

Показать, что первый частный случай всегда можно свести ко второму.

Основная идея при рассказе об уравнениях равновесия для плоской произвольной системы сил в том, что, так как П (сила) не может уравновесить пару (М), то для равновесия плоской произвольной системы сил необходимо, чтобы П=0 и М=0, т. е.

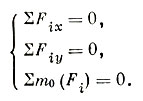
Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы выполнялись эти три уравнения.

Дать намек, что первые два уравнения накладывают "запрет" на сдвиг по осям х и цл а последнее - "запрет" поворота. О - произвольная точка, относительно которой берутся моменты всех сил, а не начало координат, как иногда представляется студентам.

Подробно остановиться затем на необходимости и достаточности уравнений равновесия. Опыт экзаменов показывает, что многие студенты плохо представляют себе, в чем необходимость и в чем заключается достаточность этих трех уравнений как условий равновесия плоской произвольной системы сил.

Существуют различные виды систем трех уравнений равновесия:

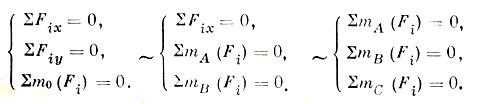
Относительно двух последних систем уравнений равновесия ставятся определенные условия, например, точки А, В и С не должны лежать на одной прямой.

Здесь может возникнуть вопрос: что "главнее" - момент или сила? Ведь есть такая система уравнений, в которую входят одни моменты, но нет такой системы, где бы не было по крайней мере одного уравнения моментов. Некоторые студенты, опираясь на это, приходят к выводу, что момент "важнее" силы. Другие говорят, что сила "важнее" момента, так как без силы нет и не может быть момента.

Сама постановка вопроса о том, что "важнее" - момент или сила, неправомерна. Сила и момент - это характеристики различных механических явлений. Сравнивать их нельзя, как нельзя сравнивать такие различные вещи, как яблоки и автомобили. В механике момент заведует вращением, а сила - "тащением" тела.

Затем рассказывается теорема Вариньона, ранее не нужно. Разбирая сложное равновесие, сначала обязательно надо рассмотреть равновесие в целом, а потом уже части.