ТЕОРИЯ ИНФОРМАЦИИ

ТЕОРИЯ ИНФОРМАЦИИ - общая теория связи, рассматривающая способы оценки количества информации, передаваемой по каналам связи или хранящейся в памяти (запоминающих устройствах). Т. и. - существенная часть кибернетики. Под информацией понимаются любые сведения, являющиеся объектом передачи, хранения и преобразования. Переработка воспринятой информации в сигналы, направляющие деятельность машин и организмов, называется управлением, а сами процессы восприятия информации, её передачи и хранения - связью. Осн. задачей связи является точное или приближённое воспроизведение в нек-ром месте сообщения, выбранного для передачи в другом месте. Под сообщением понимается любая форма передачи информации, напр. текст, речь, изображение, музыка, цифровые данные. В системах связи можно выделить 5 частей (рис. 1): 1) Источник информации, создающий сообщение или последовательность сообщений, к-рые должны быть переданы на выход системы. 2) Передатчик, к-рый перерабатывает сообщения в сигналы, соответствующие характеристикам канала. 3) Канал связи, т. е. среда, используемая для передачи сигнала от передатчика к приёмнику. 4) Приёмник, восстанавливающий переданное сообщение по полученным сигналам. 5) Адресат, или получатель информации, - лицо или аппарат, к-рому предназначено сообщение. Если рассматривать систему связи "учитель и уч-ся", то мозг и память учителя (а также уч. программа и лит-pa по рассматриваемому вопросу) являются источником информации; его эфферентные нервы и органы речи, когда он говорит, или пальцы руки, когда он пишет на доске, - передатчиком; воздушная среда, проводящая звуковые волны, или луч света - каналом связи; уши или глаза уч-ся и их слуховые или зрительные нервы - приёмником; а их мозг и память - получателем информации. Характерной особенностью процесса передачи сигналов является присоединение к передаваемому сигналу того, что не было предусмотрено источником информации. Такие нежелательные дополнения, искажения и ошибки называют помехами или шумом.

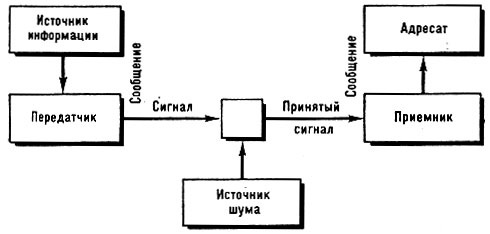
Рис. 1. Общая схема системы связи (по Шеннону)

Важнейшая проблема Т. и. заключается в определении наилучших методов, с помощью к-рых из сигнала, содержащего помехи, может быть извлечено сообщение, посланное отправителем. Одним из осн. понятий Т. и. является энтропия как мера неопределённости ситуации (случайной величины) х; с конечным или счётным числом исходов её величина равна (формула К. Шеннона) Н(х) = -Σр(х_i) log р(х_i), где р(х_i) - вероятность исхода хi, а суммирование ведётся по всем исходам. Если эти вероятности равны, то величина энтропии при заданном числе исходов является максимальной и формула принимает более простой вид: H(х) = log n, где n - число исходов, выборов или длина алфавита передаваемых сигналов. Под алфавитом понимается множество возможных сигналов (символов, стимулов), к к-рому относятся и из к-рого отбираются передаваемые сигналы, несущие информацию. Количество информации рассматривается как мера уменьшения неопределённости ситуации х (возникающего вследствие того, что становятся известными исходы другой ситуации у), усреднённая по исходам х и у. В случае ситуаций с конечным или счётным числом исходов её величина равна

I (x, y)=ΣΣ p (x_i, y_k) log	p (x_i, y_k)

	p (x_i) p (y_k)

где р (x_i, y_k) - совместная вероятность исходов х_i и y_k.

Количество информации - это мера той неопределённости, к-рая снимается после получения сообщения. Единицей количества информации является двоичная единица, или "бит", - такое количество информации, к-рое соответствует выбору одной из двух равновероятных взаимоисключающих возможностей. Предположим, что имеется система связи с последовательностями сигналов (символов, стимулов), отобранных из алфавита (х₁, х₂, х₃, х₄), на входе и последовательностями принятых сигналов (у₁, у₂, у₃, у₄) на выходе. Это может быть в равной мере и телеграфная связь с четырьмя возможными символами на входе и на выходе, и опознание с какими-то знаками на входе и ответами испытуемого или вычислительного устройства на выходе, и чтение с буквами на входе и произнесёнными звуками на выходе, и запоминание с предъявленными и воспроизведёнными символами, и письмо под диктовку со звуками на входе и написанными буквами на выходе, т. е. любые стимулы, предъявляемые человеку (или автоматич. устройству), и его ответы на эти стимулы. Предположим также, что вероятности стимулов на входе и ответов на выходе этой системы распределяются так, как это видно из рис. 2, представляющего матрицу отдельных наблюдаемых вероятностей совместного появления стимула и ответа [р (х, у)], т. е. вероятностей, с к-рыми каждый ответ даётся на каждый сигнал. Столбцы при этом представляют альтернативные стимулы (х), а строки - альтернативные ответы (у). На полях матрицы по горизонтали даны суммы вероятностей р (х), а по вертикали - суммы вероятностей р (у). Непосредственно из данных опыта, представленных в этой матрице, можно получить оценку неопределённости на входе и на выходе и совместной неопределённости входа и выхода этой системы связи:

Н(х) = - Σ p(x)log р(х) =2,00 двоичных ед.,

H(у) = - Σ p(y)log р(у) =1,99 двоичных ед.,

H(х,у) = - Σ p(x,y)logp (х,у) = 3,01 двоичных ед.

На основании теорем, доказанных в Т. и., можно также определить: а) количество информации, переданной с входа на выход системы связи, от стимула к ответу: I (х, у) = H (х) + H (у) - H (х, у) = 0,98 двоичных ед.; б) условную неопределённость сигнала, когда известен ответ, или ненадёжность передачи, т. е. потерянную при передаче информацию: Н_у (х) = Н (х, у) - H (у) = H (х)-I (х, у)=1,02 дв. ед.; в) условную неопределённость ответа, когда известен сигнал, или неоднозначность передачи, т. е. добавленную при передаче неопределённость или шум: Н_х (у) = H (х, у) - H (х) = H (у) - I (х, у) = 1,01 дв. ед. Наглядно все эти соотношения показаны на рис. 3. В случае, когда передача информации происходит без помех: I (х, у) = H (х) = H (у) = H (х, у). В случае, когда передача информации отсутствует: H (х, у) = H (х) + H (у).

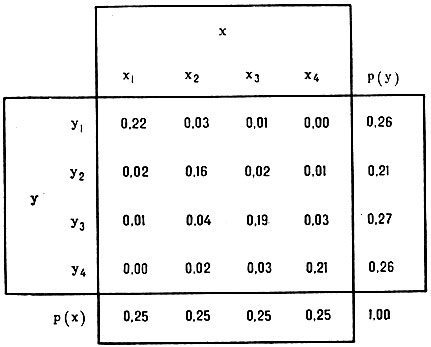
Рис. 2. Пример конкретных вероятностей, к-рые могут быть получены в опыте, где 4 альтернативных стимула в случайном порядке предъявляются испытуемым много раз

Рассмотренная передача информации относится к наиболее простому случаю двух переменных, однако этот анализ может быть распространён на любое число параметров, к-рое допускают экспериментальные и вычислительные возможности. К двум переменным "стимул" и "ответ" можно прибавить третью, напр. "испытуемые". При этом информационный анализ может показать, напр., сколько информации о стимуле содержит ответ данного испытуемого по сравнению с ответом неопределённого испытуемого (т. е. сколько информации о стимуле прибавит сообщение о том, кто давал ответ на этот стимул), или сколько информации об испытуемом, давшем ответ на неопределённый стимул, содержится в этом ответе по сравнению с ответом на данный стимул. Круг параметров, на к-рые можно распространить информационный анализ, очень широк, и оценки параметров не обязательно должны быть количественными; они могут быть и качественными, но обязательно альтернативными. Можно, напр., имея лишь качественные оценки таких параметров, как память, сообразительность и успеваемость группы уч-ся, при помощи информационного анализа узнать: сколько информации о памяти или о сообразительности содержится в оценках успеваемости, сколько информации о сообразительности содержится в данных об успеваемости, когда особенности памяти известны, и т. п.

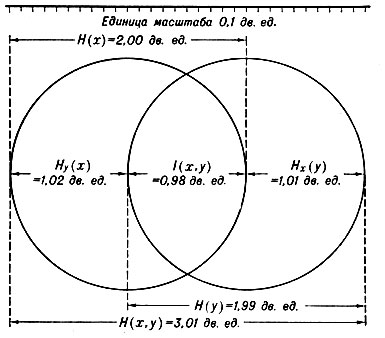
Рис. 3. Отношения между информационными компонентами при двух переменных

Термин "информация" в Т. и. не следует смешивать с термином "смысл", т. к. всякая мысль содержит информацию, но информацию может нести и не только мысль - информацию несёт и морская волна, и структура земной коры и т. п. Сообщения, из к-рых одно имеет глубокий смысл, а другое является полной бессмыслицей, могут содержать одно и то же количество информации. Больше того, бессмысленные сочетания букв с точки зрения Т. и. содержат больше информации, чем осмысленные слова. Это объясняется тем, что множество всех возможных осмысленных слов меньше множества сочетаний букв того же алфавита. Так, из букв рус. алфавита можно составить неск. тысяч осмысленных шестибуквенных слов и миллиард всевозможных шестибуквенных сочетаний. Информация же является отражением связи данного сообщения с тем множеством возможных сообщений, к к-рому оно относится, из к-рого было отобрано. Поэтому количество информации является выражением не столько того, что мы говорим, сколько того, что мы могли бы сказать, т. к. количество информации - это мера свободы выбора сообщений. Общим признаком всякой информаций является адекватная источнику пространственно-временная организация физич. состояний сигнала (носителя информации) независимо от того, применяется ли это понятие в теории связи, в теории автоматов, при исследовании проблемы чувственного образа в психологии или при управлении процессом обучения в педагогике. Природа же всякой помехи или шума, потерь информации, ненадёжности и неоднозначности её передачи заключается в разрушении адекватной источнику организации состояний её носителя.

Исходя из того, что информация является содержанием всякой мысли и лежит в основе всякой умственной деятельности, процесс обучения можно рассматривать как процесс передачи информации, а информацию как то, что учитель сообщает уч-ся, а уч-ся усваивают в процессе обучения. Поэтому применение Т. и. к изучению пед. явлений заключается в исследовании объективных закономерностей получения, передачи, переработки, хранения и использования информации в процессе обучения. Дело, конечно, не в том, чтобы информационными понятиями заменить (перекодировать) понятия педагогические, а в том, чтобы ввести количественные меры там, где раньше применялись лишь качественные понятия, давать оценку пропускной способности канала "учитель - уч-ся", находить способы наилучшего кодирования информации, увеличивающие скорость передачи информации, циркулирующей между учителем и уч-ся, и уменьшать её потери. Задача информационного подхода к педагогике заключается в такой организации познавательной деятельности уч-ся, при к-рой они могли бы переработать наибольшее количество информации за наименьшее время; в выявлении условий, при к-рых количество перерабатываемой информации является наибольшим. В таком подходе на долю самой Т. и. падает, конечно, только количественная оценка полученной информации. Но именно это и позволяет распознать преимущества одних методов обучения перед другими. В частности, Т. и. используется для построения рациональных алгоритмов решения задач, т. е. для нахождения умственных операций, обладающих большей информативностью, что зависит от информативности соответствующего признака, а последняя оценивается через ту неопределённость, к-рая снимается при его проверке. Для нахождения рациональных алгоритмов из всех возможных последовательностей признаков выбирается такая, к-рая обеспечивает получение наибольшей информации на каждый признак и благодаря этому даёт возможность решить задачу с помощью наименьшего числа операций. Т. и. позволяет также подойти к формулированию нек-рых объективных показателей степени трудности задачи, одним из к-рых является неопределённость ситуации. Т. о., осн. понятия Т. и. могут быть использованы не только для описания процесса обучения, но и для количественной оценки этого процесса и создания математич. моделей обучения. Однако введение в педагогику информационных понятий связано с трудностями (см. Кибернетика). Важно подчеркнуть, что применение этих понятий не должно предполагать отождествления процессов переработки информации человеком и соответствующих процессов в технич. системах.

Возникнув в 1948 как "математическая теория связи" К. Шеннона, Т. и. сразу же нашла применение в психологии. В настоящее время число психологич. исследований, выполненных с применением Т. и., настолько велико, что нек-рые авторы считают возможным говорить о "психологической Т. и." как о самостоятельной области знаний. Однако большинство этих исследований связано гл. обр. с изучением сенсорных процессов, включая и процессы восприятия. Что же касается более сложных психич. процессов (памяти, воображения, мышления), то здесь, так же как и в педагогике, применение Т. и. сталкивается с большими трудностями, причина к-рых - сложность объекта исследований и ограниченность совр. Т. и., к-рая рассматривает понятие информации лишь с количественной стороны. Изучение качественного своеобразия различных видов информации только начинается.

В первые годы после возникновения Т. и. большинство зарубежных ученых относилось к ней как к частному достижению в области теории связи, не представляющему интереса для математики. В СССР раньше, чем в других странах, оценили глубокое математич. содержание этой теории. Первоначально сов. ученые исходили из того, что шенноновское определение количества информации опирается на понятие вероятности, и рассматривали Т. и. как часть теории вероятностей. Сейчас, как полагает А. Н. Колмогоров, кажется более естественным принять в качестве осн. понятия именно понятие информации и затем уже на этой базе ввести понятие вероятности и строить всю теорию вероятностей.

Лит.: Харкевич А. А., Очерки общей теории связи, М., 1955; его же, О ценности информации, "Проблемы кибернетики", 1960, № 4; Колмогоров А. Н., Теория передачи информации, М., 1956; Голдман С., Теория информации, пер. с англ., М., 1957; Яглом А. М., Яглом И. М., Вероятность и информация, 2 изд., М., 1960 (им. библ.); Бриллюен Л., Наука и теория информации, пер. с англ., М., 1960; Файнстейн А., Основы теории информации, пер. с англ., М., 1960; Автоматич. управление, пер. с англ., М., 1961; Ахманова О. С. [и др.], О точных методах исследования языка, М., 1961; Бонгард М. М., О понятии "полезная информация", в сб.: Проблемы кибернетики, М., 1963, в. 9; Шапиро С. И., Уманский Л. И., О применении теории информации к изучению способностей человека, "Вопросы психологии", 1963, № 2; Эшби У. Р., Системы и информация, "Вопросы философии", 1964, № 3; Шеннон К., Работы по теории информации и кибернетики, пер. с англ., М., 1963 (им. библ.); Леонтьев А. Н. и Кринчик Е. П., Нек-рые особенности процесса переработки информации человеком, в кн.: Кибернетика. Мышление. Жизнь, М., 1964; Миллер Дж. А., Магическое число семь плюс или минус два. О нек-рых пределах нашей способности перерабатывать информацию, в сб.: Инженерная психология, пер. с англ., М., 1964; Веккер Л. М., Восприятие и основы его моделирования, Л., 1964; Ительсон Л. Б., Математич. и кибернетич. методы в педагогике, М., 1964; Теория информации. Терминология, М., 1964; Инженерная психология. Сб. статей, пер. с англ., М., 1964; Колмогоров А. Н., Проблемы теории вероятностей и математич. статистики, "Вестник АН СССР", 1965, № 5; Невельский П. Б., Объём памяти и количество информации, в сб.: Проблемы инженерной психологии, в. 3, Л., 1965; О нек-рых вопросах совр. математики и кибернетики. Сб. статей в помощь учителю математики, М., 1965; Земан И., Познание и информация, пер. с чеш., М., 1966; Ломов Б. Ф., Человек и техника, М., 1966; Концепция информации и биологич. системы, пер. с англ., М., 1966; Ланда Л. Н., Алгоритмизация в обучении, М., 1966 (им. библ.); Моль А., Теория информации и эстетич. восприятие, пер. с франц., М., 1966 (им. библ.); Бочарова С. П., Память и ценность информации, в сб.: Память и деятельность (XVIII Международный психологический конгресс, Симпозиум 22), М., 1966; Урсул А. Д., Нестатистич. подходы в теории информации, "Вопросы философии", 1967, № 2; Garner W. R., Hake Н. W., The amount of information in absolute judgments, "Psychological Review", 1951, № 58, p. 446 - 59; Mc Gill W. J., Multivariate information transmission, "Psychometrika", 1954, v. 19, p. 97 - 116; Quastler H. [ed.], Information theory in psychology. Problems and methods, Glencoe (Ill.), 1956, Garner W. R., Mc Gill W. J., The relation between information and variance analysis, "Psychometrika", 1956, v. 21, p. 219 - 28; Attneave F., Applications of information theory to psychology: a summary of basic concepts, methods and results, N. Y., 1959; Frank H., Kybernetische Grundlagen der Pädagogik, Baden-Baden - P., 1962 (рус. пер. в печати); Garner W. R., Uncertainty and structure as psychological concepts, N. Y.- L., 1962; Сlauβ G., Zur Handlungsanalyse durch Algorithmen und ihre Anwendung im Unterricht, "Paädagogik", 1965, № 4.