Немного теории

Почему взлетает воздушный змей? Ответить на этот вопрос поможет упрощенный чертеж (рис. 1). Пусть линия AB изображает разрез плоского змея. Предположим, что змей взлетает справа налево под углом а к горизонту или набегающему потоку ветра. Рассмотрим, какие силы действуют на модель в полете. На взлете плотная масса воздуха препятствует движению змея, другими словами, оказывает на него некоторое давление. Обозначим силу давления 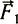. Теперь построим так называемый параллелограмм сил и разложим силу 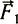на две составляющие - 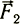и . 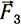Сила 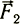толкает змей от нас, а это значит, что при подъеме она снижает его первоначальную горизонтальную скорость. Следовательно, это сила сопротивления. Другая сила 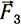увлекает змей вверх, поэтому назовем ее подъемной.

Итак, мы определили, что на воздушный змей действуют две силы: сила сопротивления 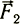и подъемная сила 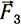. Поднимая модель в воздух (буксируя ее за леер), мы как бы искусственно увеличиваем силу давления на поверхность змея, т. е. силу 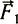. И чем быстрее мы разбегаемся, тем больше становится эта сила. Но сила 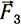как вы уже знаете, раскладывается на две составляющие: 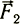и 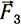. Масса модели постоянна, а действию силы 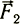препятствует леер. Значит, увеличивается подъемная сила - змей взлетает.

Известно, что скорость ветра с высотой возрастает, ведь чем выше от земли, тем меньше предметов, которые препятствовали бы его движению. Вот почему при запуске стараются поднять змей на такую высоту, где ветер мог бы его поддерживать.

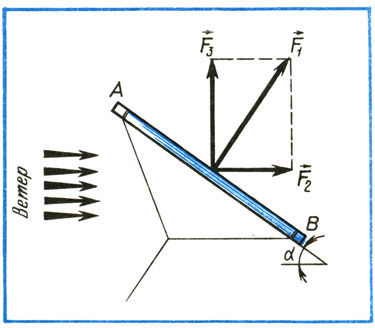
Рис. 1. Разрез плоского змея и силы, действующие на него

В полете змей всегда находится под определенным углом к направлению ветра. Понять это поможет простой опыт. Возьмите прямоугольный лист картона (рис. 2). Точно по центру прикрепите его к оси OO. Предположим, что лист вращается вокруг оси без трения и в любом положении находится в состоянии равновесия. Допустим также, что ветер дует с постоянной силой перпендикулярно плоскости листа. В этом случае он не может повернуть лист вокруг оси OO, поскольку действие его распределяется равномерно на весь лист. Теперь попробуйте установить лист под некоторым углом к ветру. Вы увидите, как воздушный поток тотчас возвратит его в первоначальное положение, т. е. поставит под прямым углом к направлению своего действия. Это значит, что из двух равных частей листа, разделенных осью OO, большее давление испытывает та часть, которая наклонена в сторону ветра. Поэтому, чтобы плоскость листа оставалась в наклонном положении, нужно поднять ось вращения OO. Чем меньше угол наклона листа, тем выше нужно передвинуть ось. Так определяется центр давления. А сила ветра, поддерживающая плоскость в наклонном положении, - это подъемная сила, приложенная в центре давления. Но угол наклона змея не остается постоянным: ведь ветер никогда не дует с одной и той же скоростью. Вот почему, если бы мы привязали к змею бечевку (дальше ее будем называть леером) в одной точке, например в точке совпадения центра давления и центра тяжести, он начал бы кувыркаться в воздухе. Как вы уже поняли, положение центра давления зависит от угла а, и при порывистом ветре эта точка постоянно смещается. Поэтому, чтобы сделать модель более устойчивой, между ней и леером привязывают уздечку из двух-трех и более бечевок.

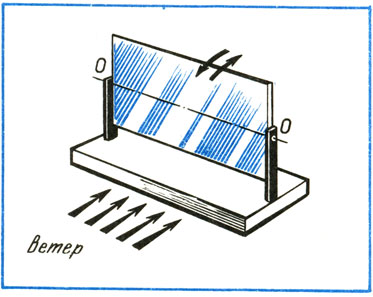
Рис. 2. Опыт, демонстрирующий возникновение подъемной силы

Проделайте еще один опыт. Возьмите палочку AB (рис. 3, а). Пусть она символизирует сечение плоского змея. Подвесьте ее за нитку в центре так, чтобы она приняла горизонтальное положение. Затем прикрепите недалеко от центра тяжести O грузик. Действующий с силой R, имитирующий центр давления. Палочка сразу же потеряет равновесие и примет почти вертикальное положение. А теперь попробуем эту палочку подвесить на двух нитках, как показано на рис. 3, б, и снова привяжем к ней тот же грузик: палочка будет сохранять равновесие независимо от положения грузика. Этот пример наглядно демонстрирует роль уздечек, которые позволяют центру давления свободно перемещаться, не нарушая равновесия.

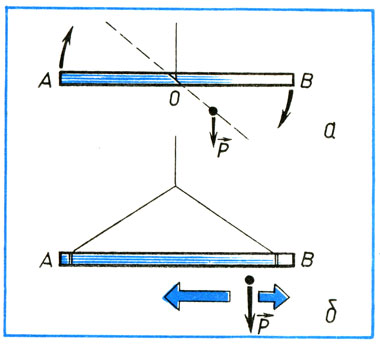
Рис. 3. Опыты, показывающие неустойчивое (а) и устойчивое (б) закрепление палочки (змея) к уздечке

На примерах нескольких простейших моделей легко уяснить положения, объясняющие полет воздушных змеев. Описание конструкций этих моделей дано ниже. Одни из них можно изготовить за час-два, а другие - всего за несколько минут. Такие змеи хорошо летают и не требуют сложного управления. Итак, сначала...