§ 23. Способы определения натуральной величины отрезка прямой линии и плоской фигуры

Элементы деталей, наклонные к плоскостям проекций, проецируются на них с искажением размеров. Однако в некоторых случаях требуется получить на чертеже натуральную величину отрезков прямых линий или плоских фигур, в частности при построении разверток.

Натуральные размеры отрезков линий и фигур получаются на той плоскости проекций, параллельно которой они расположены. Следовательно, чтобы определить натуральную величину отрезка линии или фигуры, необходимо, чтобы плоскость проекции была параллельна изображаемому элементу. Для этого применяют способ вращения и способ перемены плоскостей проекций.

Способ вращения. Способ вращения заключается в том, что отрезок прямой линии или плоскую фигуру вращают вокруг выбранной оси до положения, параллельного плоскости проекций.

На рис. 173 показано, как определить способом вращения натуральную длину отрезка АВ прямой, наклонной к плоскостям проекций. На наглядном изображении (рис. 173, а) видно, что отрезок А В прямой не параллелен плоскостям проекций и, следовательно, проекции а'b' и ab отрезка изображаются искаженными. Нужно повернуть отрезок вокруг оси Аа, перпендикулярной к плоскости H, в направлении, указанном стрелкой, до положения, при котором отрезок станет параллельным плоскости V, т. е. в положение, обозначенное АВ₁. Тогда горизонтальная проекция аb отрезка АВ расположится параллельно плоскости V (параллельно оси х); обозначим ее аb₁. В этом положении проекция отрезка на плоскость V - линия а'b' представляет собой натуральную величину отрезка АВ.

Построение на чертеже начинают с горизонтальной проекции (рис. 173, б). Из точки а, как из центра, радиусом, равным ab, описывают дугу окружности bb₁ до пересечения с прямой, проведенной из точки а параллельно оси х. Получают новую горизонтальную проекцию b₁ точки В. Фронтальную проекцию b`<sub>1</sub> точки b<sub>1</sub> получают, восставив из нее перпендикуляр к оси х. Соединив прямой точку а' с точкой b` получают натуральную длину отрезка АВ.

На рис. 173, в показано, как можно данное построение применить к определению натуральной длины наклонного ребра треугольной пирамиды.

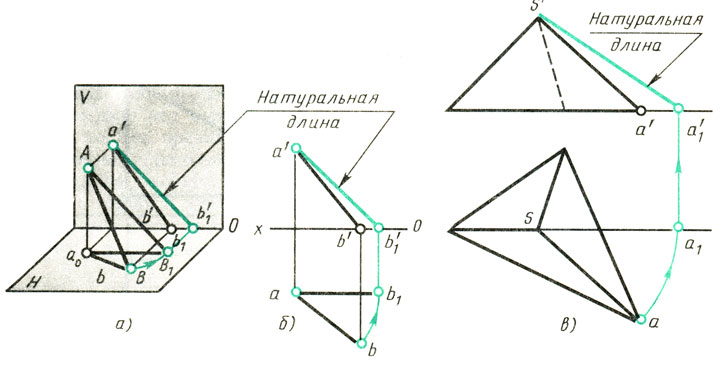
Рис. 173. Определение натуральной длины отрезка прямой способом вращения

Способ перемены плоскостей проекций. Этот способ отличается от способа вращения тем, что проецируемая линия или фигура остается неподвижной, а одну из плоскостей проекций заменяют новой дополнительной плоскостью, на которую и проецируют изображаемый элемент.

В пересечении новой плоскости Н₁ с плоскостью V (рис. 174, а) получают новую ось проекций х₁. Новую систему плоскостей на чертеже обозначают H₁/V

Дополнительную плоскость проекций Н₁ выбирают так, чтобы она была перпендикулярна фронтальной плоскости проекций V (рис. 174, а) и параллельна линии или плоскости фигуры, натуральную величину которой нужно определить. Линия или фигура спроецируется на дополнительную плоскость без искажений; новая ось проекций хх будет параллельна фронтальной проекции наклонной грани (рис. 174, б).

Рассматривая рис. 174, а и б, можно установить, что при перемене горизонтальной плоскости Н на новую Н₁ расстояние новой горизонтальной проекции любой точки до оси проекций х¹ будет равно расстоянию прежней горизонтальной проекции этой точки до прежней оси проекций, т. е. расстояние точки А от плоскости V остается неизменным. Этим и пользуются при построении проекций фигур на дополнительную плоскость, которую затем совмещают с плоскостью чертежа.

На рис. 174, а точка А спроецирована сначала на плоскости V и H, т. е. получены ее проекции а' и а. Затем взята дополнительная плоскость H₁ перпендикулярная к плоскости V, и точка А спроецирована на дополнительную плоскость. Для этого из фронтальной проекции a` до точки А опущен перпендикуляр на плоскость H₁ пересечение которого с плоскостью дало точку ах₁. Затем от точки аx₁ отложено расстояние, равное аа_х, и получена искомая проекция a₁ точки А на дополнительную плоскость. Наклонная линия x₁ на чертеже обозначает новую ось проекций. Важно отметить, что фронтальная и новая проекции точки А лежат на одном перпендикуляре к оси х₁.

На рис. 174, б дано наглядное изображение четырехугольной призмы, верхняя грань которой наклонна. Чтобы определить натуральную величину верхней наклонной грани призмы, ее необходимо спроецировать на дополнительную плоскость. Построение проводят в следующем порядке. Вычерчивают фронтальную и горизонтальную проекции призмы. На произвольном расстоянии проводят новую ось проекции х₁ параллельно фронтальной проекции изображаемой грани. Из фронтальных проекций вершин наклонной грани - точек а`, b`, с`, d' восставляют перпендикуляры к новой оси x₁. На перпендикулярах от новой оси х₁ откладывают отрезки, равные расстояниям горизонтальных проекций этих точек от оси х. Соединив полученные точки а₁, b₁, с₁, d₁ прямыми линиями, получают натуральную величину грани.

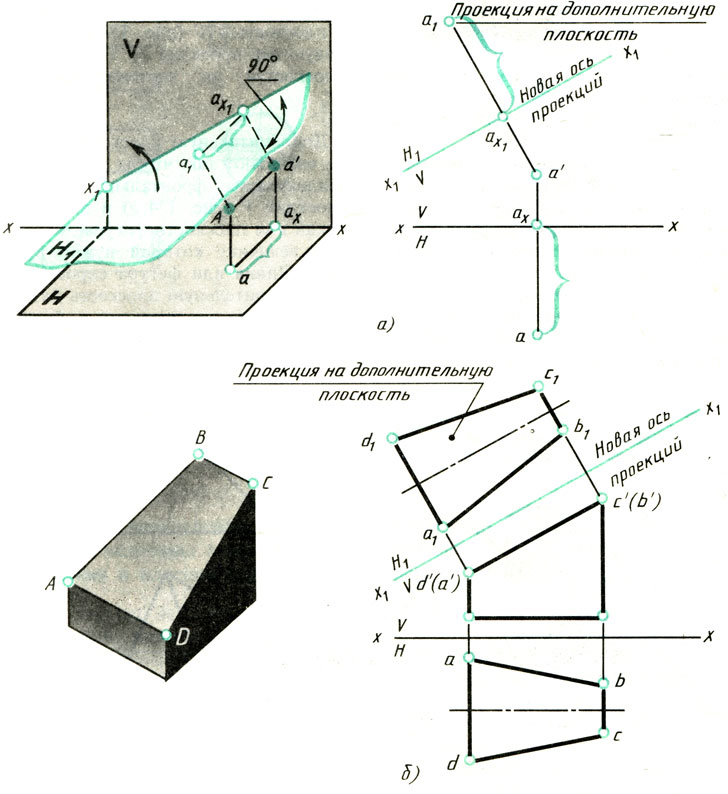
Рис. 174. Определение натуральной величины фигуры способом перемены плоскостей проекций

Изображение детали на дополнительной плоскости называют дополнительным видом, который отмечают на чертежах надписью типа "Вид А", "Вид Б", подчеркнутой тонкой линией. У связанного с дополнительным видом изображения наносят стрелку, указывающую направление взгляда, с соответствующим буквенным обозначением (рис. 175, a), при этом выбирают одну из прописных букв русского алфавита. Дополнительный вид допускается повертывать, но, как правило, с сохранением положения, принятого для данного предмета на главном изображении, при этом к надписи "Вид Б" должно быть добавлено слово "повернуто", располагаемое в строчку с надписью (рис. 175, б). Когда дополнительный вид расположен в непосредственной проекционной связи с соответствующим изображением, стрелку и надпись над видом не наносят (рис. 175, в).

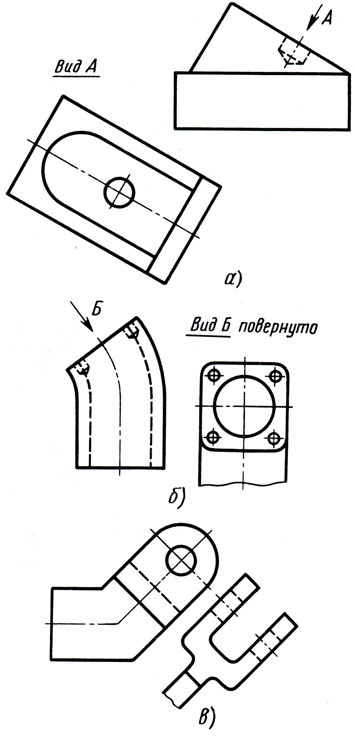
Рис. 175. Расположение и обозначение дополнительных видов

Ответьте на вопросы

1. Как обозначают на чертежах дополнительные виды?

2. Чем отличается способ вращения от способа перемены плоскостей проекции? Для чего эти способы применяются?