§ 10. Лекальные кривые

В технике встречаются детали, поверхности которых образованы перемещением кривых линий: эллипса, эвольвенты окружности, спирали Архимеда и др. Кривые линии нельзя точно вычертить циркулем, поэтому отдельные точки этих кривых соединяют плавными линиями при помощи лекал. Отсюда название - лекальные кривые.

Эвольвента окружности. На рис. 71 приведена эвольвента окружности. Каждая точка прямой, если ее катить без скольжения по окружности, описывает эвольвенту.

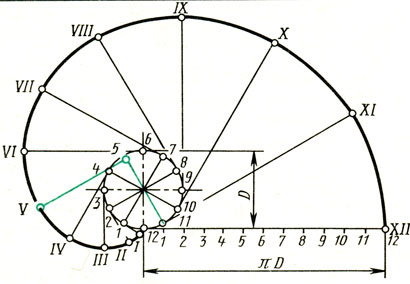
Рис. 71. Эвольвента окружности

Профиль рабочих поверхностей зубьев большинства зубчатых колес имеет эвольвентное очертание (рис. 72).

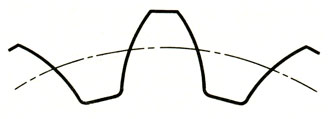
Рис. 72. Эвольвентный профиль зуба

Спираль Архимеда. На рис. 73 изображена спираль Архимеда. Это плоская кривая, которую описывает точка, равномерно движущаяся от центра О по равномерно вращающемуся радиусу.

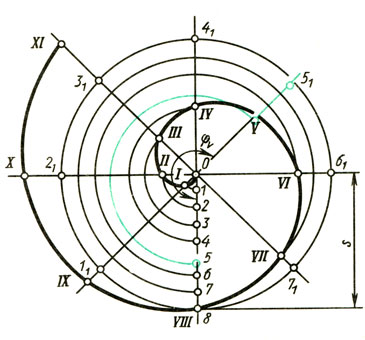
Рис. 73. Спираль Архимеда

По спирали Архимеда нарезают канавку, в которую входят выступы кулачков самоцентрирующего трехкулачкового патрона токарного станка (рис. 74). При вращении конической шестерни, на обратной стороне которой нарезана спиральная канавка, кулачки перемещаются.

При построении лекальных кривых на чертеже можно воспользоваться справочником, чтобы вспомнить, как это делается.

Рис. 74. Спираль Архимеда на тыльной стороне зубчатого колеса токарного патрона

Построение эллипса. Размеры эллипса определяются величинами его большой АВ и малой CD осей (рис. 75). Описывают две концентрические окружности. Диаметр большей равен длине эллипса (большой оси АВ), диаметр меньшей - ширине эллипса (малой оси CD). Делят большую окружность на равные части, например на 12. Точки деления соединяют прямыми, проходящими через центр окружностей. Из точек пересечения прямых с окружностями проводят линии, параллельные осям эллипса. При взаимном пересечении этих линий получают точки, принадлежащие эллипсу, которые соединяют от руки плавной кривой и обводят по лекалу.

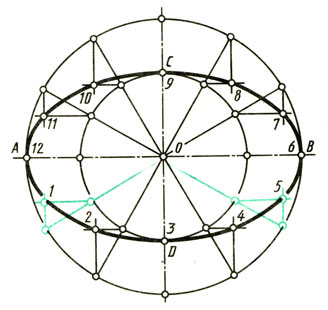
Рис. 75. Построение эллипса