Принцип возможных перемещений

Как известно, принцип виртуальных (пробных) перемещений гласит: "Для равновесия системы с идеальными а неподвижными связями необходимо и достаточно, чтобы сумма работ одних только активных сил на всяком виртуальном перемещении равнялась нулю". Или математически: ∑(Fδr)=0.

В статике мы учим студентов, что для равновесия необходимо и достаточно, чтобы сумма всех сил равнялась нулю, а Лагранж говорит о сумме работ. Почему?

Если точка свободная, то для нее нет смысла писать принцип возможных перемещении. Если точка несвободная, то появляются реакции, и, следовательно, в статике надо учитывать все силы: и активные, и пассивные.

А Лагранж говорит: "Моему принципу все равно - свободная точка или не свободная. Реакции на идеальных связях не работают".

Понимать принцип Лагранжа надо так. Точка находится в покое, если окрестности ее одинаковы Устойчивое Неустойчивое и ей все равно, куда двигаться. Одинаково двигаться - значит одинаково работать. Именно поэтому Лагранж сформулировал свой принцип, как принцип работ. Точка лежит на поверхности (рис. 27) и как бы мысленно выпускает щупальца и пробует окрестности вокруг себя. Если окрестности одинаковы и ей все равно, куда двигаться, она остается на месте. Пробы надо делать малые. Иначе возможно нарушение равновесия (рис. 28).

Рис. 27

Представьте себе, что вы сброшены ночью на парашюте в незнакомой местности. Приземлились и стоите в абсолютной темноте. Ничего не видно. Решитесь ли вы сразу пойти? Нет, конечно. Будете бояться. В таком положении вы как слепой. Вы начнете делать "виртуальные перемещения". Вы их не делаете сами, а палкой пробуете окрестности вокруг себя. Вот это и есть δr.

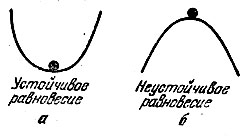
Рис. 28

Несколько слов о термине "принцип возможных перемещений". Его можно объяснить, но сбивает с толку слово "возможные". Если точка, "сидит" на освобождающей связи, то покидание связи тоже возможно. Надо объяснить, что термин "возможные перемещения" означает бесконечно малые перемещения, согласные со связями (без их покидания). Чтобы не создавать превратного представления, говорят "виртуальные перемещения". Но тогда слушателей поражает иностранное слово. Его надо перевести на русский язык. По-латыни "виртус" - добродетель, "вир" - мужчина. Как эти значения связать с принципом Лагранжа? Непонятно. Поэтому лучше говорить "пробные перемещения".

Рассказывать ли самую суть механики Лагранжа? Говорить ли о том, что он первый догадался написать уравнение связей. Ведь принцип-то не его, а Бернулли. В письме к Вариньону Бернулли пишет: "Я заметил, что задача решается так..." Но как он это заметил?

Введение связей - существенный момент. По-видимому, Лагранж старается оценить состояние покоя, не столько изучая силы, сколько окрестности точки равновесия.

Материальная точка на горизонтальной плоскости находится в равновесии, а на наклонной - нет (рис. 29). В чем дело? В уравновешивании или в том, что окрестности разные? В первом случае окрестность перпендикулярна к Р, а во втором - нет. По Лагранжу, все дело в том, как окрестность расположена по отношению к силе. Механика Лагранжа исследует окрестность, отодвигая на вадиий план изучение сил. Это и надо показать. Идея сравнения - вот в чем суть механики Лагранжа. Точка не сдвигается не потому, что действует такая сила, а потому, что имеется такая окрестность. Покой, по Лагранжу, - это не покой, а страшная нерешительность. Представьте себе, что перед вами фея рассыпала билеты во все театры Москвы, и все в первый ряд. Куда вы пойдете? Наверное, никуда. Одинаково хочется пойти по разным направлениям, и остается покой. По Буридану: осел и перед ним два ведра. Куда пойдет осел? Никуда, и умирает с голоду.

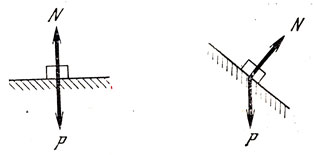
Рис. 26

Чтобы вдохнуть физическое содержание в принцип возможных перемещений, надо рассказать о той эпохе и общественно-исторических предпосылках, которые позволили Лагранжу создать свою аналитическую механику. Изложить это за короткое время трудно. Да и студенты неохотно выслушивают философско-исторические отступления. Но делать это надо.

Появление аналитической механики Лагранжа не случайно, и надо хотя бы немного представлять себе, как это происходило. Лагранж создает свою книгу в эпоху, характерную новыми открытиями в разных областях науки. В астрономии назрела необходимость вычислить либрацию Луны, но это плохо удается при помощи ньютоновской механики. Начинают сомневаться в справедливости механики Ньютона. Состояние отчаяния заставляет Берлинскую академию наук объявить конкурс на сочинение "Истины необходимые и ненеобходимые". Рациональные истины считают неопровержимыми. А не чисто рациональные? Взятые из опыта? Наука это или нет?

В то время стала укореняться мысль, что основы механики Ньютона случайны. Они эмпиричны, и, может быть, поэтому ньютоновская механика перестала удовлетворять ученых, так как не могла объяснить вновь обнаруженные явления природы. Одни ученые пошли по пути создания новых экстравагантных аксиом. Другие стали искать чисто рациональные принципы построения механики, так как считали, что рассудок безупречен и дает абсолютные истины. К этим последним принадлежал Лагранж. Он понимал, что для решения новых практических задач требуется создание новой более мощной механики.

Лагранж изучает историю механики, конструирует одним рассудком безупречные истины, и, боясь всякого нечистого вмешательства, изгоняет из своей аналитической механики даже чертежи. В письме к д'Аламберу Лагранж пишет, что математика скоро будет напоминать арабский язык. Д'Аламбер ополчился на понятие силы. Его трактат направлен против нечистой опытной силы. Она ему непонятна. Лагранж "засекретил" силу, введя ее в работу.

Прав Пуассон, утверждая, что возникают две школы: Ньютона и Лагранжа. Сам примыкает к Лапласу и Ньютону, а Лагранжа упрекает в том, что в его построениях нет физики. В этом он видит главную вину Лагранжа. Действительно, физики нет. Заменил ее уравнениями. В этом главная заслуга Лагранжа!